The Supply Curve

Usually, in the short run, other things equal, the supply curve is an upward sloping function of the price of the good or service being studied. For each level of output, the supply curve reveals the minimum price at which suppliers are willing to sell. Similarly, at each level of the price the supply curve reveals the maximum quantity that suppliers are willing to sell. In the case of linear expressions, a supply curve in its simplest form would be:

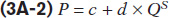
where P is the price, QS is the quantity, and c and d are positive constants.3 That d × QS is added to a constant tells us that as price rises, all else constant, a higher level of quantity is supplied and vice versa (the supply curve slopes upward). The d term describes how sensitive the price is to changes in the quantity supplied (i.e., the slope of the supply curve). If d takes on a larger value then the supply curve becomes relatively steeper—the same change in quantity results in a larger change in the minimum price at which suppliers are willing to sell. If d takes on a smaller value, the effect is opposite—the demand curve becomes relatively flatter and the same change in quantity results in a smaller change in the minimum price at which suppliers are willing to sell.

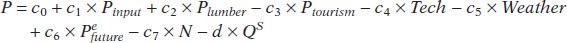
Again, the simple appearance of Equation 3A-2 hides enormous amounts of information. The constant c contains information on the factors that shift the supply curve: changes in the prices of inputs, changes in the prices of related goods and services, changes in technology, changes in weather, changes in expectations, and changes in the number of producers. For example, the supply of maple syrup, again with the price in dollars per litre and the quantity in millions of litres, might be represented by a linear supply curve such as:

with c expanded to include several factors multiplied by constants that are summarized in Table 3A-2. These factors are all multiplied by positive constants that, like d, describe how sensitive the supply curve is to change in those factors. The constant c0 picks up the impact of all other determinants of the supply of maple syrup that have been left out of the equation of the supply curve. Like the demand curve, if any of these values change, then the supply curve changes too. Figure 3A-2 examines a shift in the supply curve using algebra.

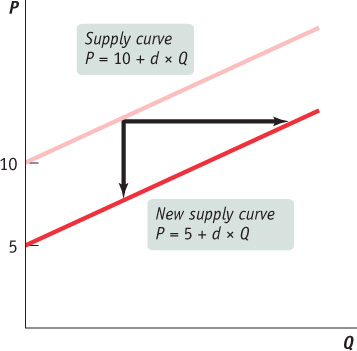
TABLE3A-2 Variable Factors That Shift Maple Syrup Supply
Figure3A-2Shifts of the Supply Curve As with the demand curve in Figure 3A-1, there are two ways to interpret a shift in the supply curve. In economics, a decrease in the value of c represents an increase in supply, which shifts the supply curve to the right. The shift right can also be seen as a shift down because the constant term decreased. In this diagram, the value of c changes from 10 to 5.
Note that if supply decreases (i.e., c increases), the supply curve shifts up (or to the left).

Suppose that, given a set of values for all the factors and constants, we get the following supply curve for maple syrup:

P = 12.75 + 0.25QS

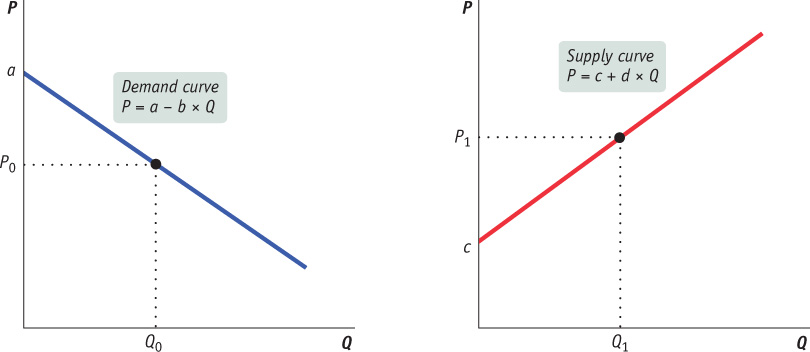
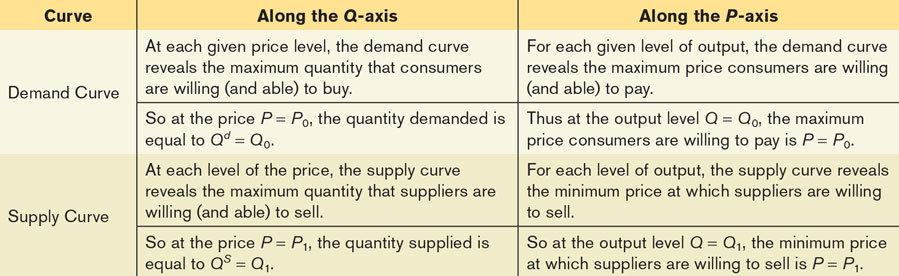
Before we use the demand and supply curves for maple syrup to find the equilibrium price and quantity, let’s look at Figure 3A-3, which provides a visual summary of the demand and supply curves. For a summary of how to interpret points along these curves, see Table 3A-3.

Figure3A-3Demand and Supply Curves In the demand curve, the term a is the P-axis intercept. This is the lowest price with zero demand. If the price falls below a, then the quantity demanded rises above zero. Similarly, in the supply curve, the term c is the P-axis intercept. This is the price that is so low, the quantity supplied falls to zero. If the price increases from c, then the quantity supplied rises above zero. The slope of the demand curve is equal to −b and the slope of the supply curve is equal to d. Table 3A-3 provides a summary of alternative interpretations of the points along the demand and supply curves.
TABLE3A-3 Interpreting Points along Demand and Supply Curves