Price Elasticity of Demand
Let’s return to our example from Appendix 3A, the demand for maple syrup, to look at the algebra of elasticity. There, we started with a very simple linear demand curve in its simplest form:
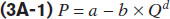
where P denotes the price (in dollars per litre), Qd denotes the quantity (in millions of litres), and a and b are positive constants.
If we isolate Qd as a function of the other terms, we get:
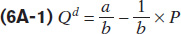
According to this equation, if the price of maple syrup increases by $1 per litre (i.e., ΔP = 1), then the quantity of maple syrup demanded decreases by 
 . Therefore, the ratio
. Therefore, the ratio 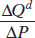 is equal to
is equal to  , a fact we will need to use later.
, a fact we will need to use later.
Now we can look more closely at the price elasticity of demand, which was expressed in Equation 6-5 as:

This equation can be simplified after rewriting it using algebraic terms such as ΔQd for the change in Qd = Q2 – Q1, ΔP for the change in P = P2 – P1, and using the values P and Qd instead of the midpoint values:
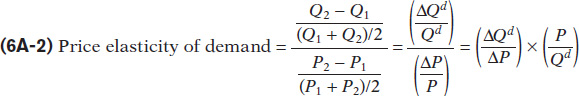
When interpreting the price elasticity of demand, we only look at the absolute value, so we can redefine the price elasticity of demand, Ed, as:

This formula for the price elasticity of demand comes in handy when analyzing a graph of the demand curve. As we move along the demand curve in Figure 6A-1, b remains constant but the ratio of P divided by Qd varies. Therefore the price elasticity of demand varies as we move along a linear demand curve. The ratio P/Qd is the slope of the line passing through the origin and the point (Qd, P) on the demand curve (because the rise of the line is P and the run is Qd). When the slope of the line is equal to b, the point at which this line intersects the demand curve has a price elasticity of demand of one—
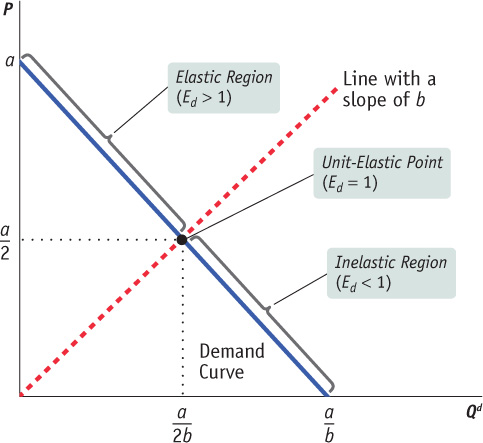
These regions can be determined algebraically by first substituting P = a – b × Qd into Equation 6A-
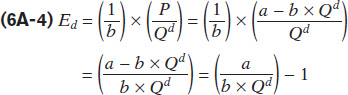
Notice that by carefully selecting values of Qd, we can generate values of Ed that are less than, greater than, or equal to 1.
If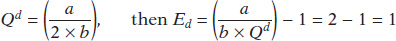
If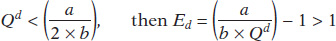
If