14.3 Games Oligopolists Play
In our duopoly example and in real life, each oligopolistic firm realizes both that its profit depends on what its competitor does and that its competitor’s profit depends on what it does. That is, the two firms are in a situation of interdependence, where each firm’s decision significantly affects the profit of the other firm (or firms, in the case of more than two).
When a firm’s decision significantly affects the profits of other firms in the industry, the firms are in a situation of interdependence.
In effect, the two firms are playing a “game” in which the profit of each player depends not only on its own actions but on those of the other player (or players). In order to understand more fully how oligopolists behave, economists, along with mathematicians, developed the area of study of such games, known as game theory. It has many applications, not just to economics but also to military strategy, politics, and other social sciences.
The study of behaviour in situations of interdependence is known as game theory.
Let’s see how game theory helps us understand oligopoly.
The Prisoners’ Dilemma
The reward received by a player in a game, such as the profit earned by an oligopolist, is that player’s payoff.
Game theory deals with any situation in which the reward to any one player—
When there are only two players, as in a duopoly, the interdependence between the players can be represented with a payoff matrix like that shown in Figure 14-2. Each row corresponds to an action by one player (in this case, Nestlé); each column corresponds to an action by the other (in this case, Mars). For simplicity, let’s assume that Nestlé can pick only one of two alternatives: produce 30 million kilograms of chocolate or produce 40 million kilograms. Mars has the same pair of choices.
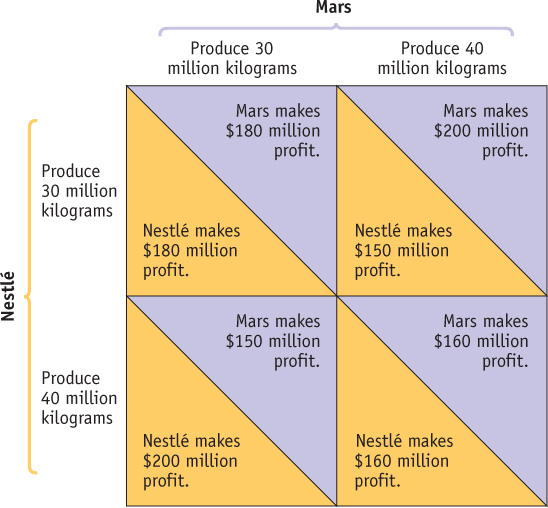
A payoff matrix shows how the payoff to each of the participants in a two-
The matrix contains four boxes, each divided by a diagonal line. Each box shows the payoff to the two firms that results from a pair of choices; the number below the diagonal shows Nestlé’s profits, the number above the diagonal shows Mars’s profits.
These payoffs show what we concluded from our earlier analysis: the combined profit of the two firms is maximized if they each produce 30 million kilograms. Either firm can, however, increase its own profits by producing 40 million kilograms while the other produces only 30 million kilograms. But if both produce the larger quantity, both will have lower profits than if they had both held their output down.
The particular situation shown here is a version of a famous—
Each player has an incentive, regardless of what the other player does, to cheat—
to take an action that benefits it at the other’s expense. When both players cheat, both are worse off than they would have been if neither had cheated.
Prisoners’ dilemma is a game based on two premises: (1) Each player has an incentive to choose an action that benefits itself at the other player’s expense (2) When both players act in this way, both are worse off than if they had acted cooperatively.
The original illustration of the prisoners’ dilemma occurred in a fictional story about two accomplices in crime—
So the police put the miscreants in separate cells and say the following to each: “Here’s the deal: if neither of you confesses, you know that we’ll send you to jail for 5 years. If you confess and implicate your partner, and she doesn’t do the same, we’ll reduce your sentence from 5 years to 2. But if your partner confesses and you don’t, you’ll get the maximum 20 years. And if both of you confess, we’ll give you both 15 years.”
Figure 14-3 shows the payoffs that face the prisoners, depending on the decision of each to remain silent or to confess. (Usually the payoff matrix reflects the players’ payoffs, and higher payoffs are better than lower payoffs. This matrix is an exception in that it shows their costs: a higher number of years in prison is bad, not good!) Let’s assume that the prisoners have no way to communicate and that they have not sworn an oath not to harm each other or anything of that sort. So each acts in her own self-
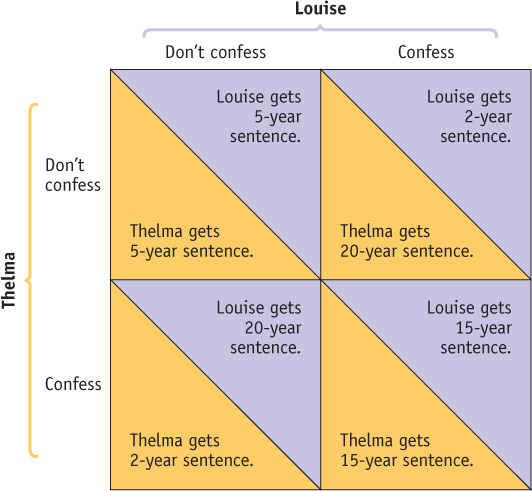
An action is a dominant strategy when it is a player’s best action regardless of the action taken by the other player.
The answer is clear: both will confess. Look at it first from Thelma’s point of view: she is better off confessing, regardless of what Louise does. If Louise doesn’t confess, Thelma’s confession reduces her own sentence from 5 years to 2. If Louise does confess, Thelma’s confession reduces her sentence from 20 to 15 years. Either way, it’s clearly in Thelma’s interest to confess. And because she faces the same incentives, it’s clearly in Louise’s interest to confess, too. To confess in this situation is a type of action that economists call a dominant strategy. An action is a dominant strategy when it is the player’s best action regardless of the action taken by the other player.
It’s important to note that not all games have a dominant strategy—
So if each prisoner acts rationally in her own interest, both will confess. Yet if neither of them had confessed, both would have received a much lighter sentence! In a prisoners’ dilemma, each player has a clear incentive to act in a way that hurts the other player—
A Nash equilibrium results when each player in a game chooses the action that maximizes his or her payoff given the actions of other players, ignoring the effects of his or her action on the payoffs received by those other players.
When Thelma and Louise both confess, they reach an equilibrium of the game. We have used the concept of equilibrium many times in this book; it is an outcome in which no individual or firm has any incentive to change his or her action. In game theory, this kind of equilibrium, in which each player takes the action that is best for her given the actions taken by other players, and vice versa, is known as a Nash equilibrium, after the mathematician and Nobel laureate John Nash. (Nash’s life was chronicled in the bestselling biography A Beautiful Mind, which was made into a movie starring Russell Crowe.) The players in a Nash equilibrium do not take into account the effect of their action on others; in a prisoners’ dilemma the Nash equilibrium is also known as a noncooperative equilibrium.
Now look back at Figure 14-2: Nestlé and Mars are in the same situation as Thelma and Louise. Each firm is better off producing the higher output, regardless of what the other firm does. Yet if both produce 40 million kilograms, both are worse off than if they had followed their agreement and produced only 30 million kilograms. In both cases, then, the pursuit of individual self-
Prisoners’ dilemmas appear in many situations. The upcoming For Inquiring Minds describes an example from the days of the Cold War. Clearly, the players in any prisoners’ dilemma would be better off if they had some way of enforcing cooperative behaviour—
But in Canada an agreement setting the output levels of two oligopolists isn’t just unenforceable, it’s illegal. So it seems that a noncooperative equilibrium is the only possible outcome. Or is it?
PLAYING FAIR IN THE PRISONERS’ DILEMMA
One common reaction to the prisoners’ dilemma is to assert that it isn’t really rational for either prisoner to confess. Thelma wouldn’t confess because she’d be afraid Louise would beat her up, or Thelma would feel guilty because Louise wouldn’t do that to her.
But this kind of answer is, well, cheating—
Luckily, when it comes to oligopoly, it’s a lot easier to believe that the firms care only about their profits. There is no indication that anyone at Nestlé felt either fear of or affection for Mars, or vice versa; it was strictly about business.
Overcoming the Prisoners’ Dilemma: Repeated Interaction and Tacit Collusion
Thelma and Louise in their cells are playing what is known as a one-shot game—that is, they play the game with each other only once. They get to choose once and for all whether to confess or hang tough, and that’s it. However, most of the games that oligopolists play aren’t one-shot; instead, they expect to play the game repeatedly with the same rivals. An oligopolist usually expects to be in business for many years, and it knows that its decision today about whether to cheat is likely to affect the way other firms treat it in the future. So a smart oligopolist doesn’t just decide what to do based on the effect on profit in the short run. Instead, it engages in strategic behaviour, taking account of the effects of the action it chooses today on the future actions of other players in the game. And under some conditions oligopolists that behave strategically can manage to behave as if they had a formal agreement to collude.
A firm engages in strategic behaviour when it attempts to influence the future behaviour of other firms.
Suppose that Nestlé and Mars expect to be in the chocolate business for many years and therefore expect to play the game of cheat versus collude shown in Figure 14-2 many times. Would they really betray each other time and again?
Probably not. Suppose that Nestlé considers two strategies. In one strategy it always cheats, producing 40 million kilograms of chocolate each year, regardless of what Mars does. In the other strategy, it starts with good behaviour, producing only 30 million kilograms in the first year, and watches to see what its rival does. If Mars also keeps its production down, Nestlé will stay cooperative, producing 30 million kilograms again for the next year. But if Mars produces 40 million kilograms, Nestlé will take the gloves off and also produce 40 million kilograms the next year. This latter strategy—start by behaving cooperatively, but thereafter do whatever the other player did in the previous period—is generally known as tit for tat.
A strategy of tit for tat involves playing cooperatively at first, then doing whatever the other player did in the previous period.
Tit for tat is a form of strategic behaviour, which we have just defined as behaviour intended to influence the future actions of other players. Tit for tat offers a reward to the other player for cooperative behaviour—if you behave cooperatively, so will I. It also provides a punishment for cheating—if you cheat, don’t expect me to be nice in the future.
The payoff to Nestlé of each of these strategies would depend on which strategy Mars chooses. Consider the four possibilities, shown in Figure 14-4:
If Nestlé plays tit for tat and so does Mars, both firms will make a profit of $180 million each year.
If Nestlé plays always cheat but Mars plays tit for tat, Nestlé makes a profit of $200 million the first year but only $160 million per year thereafter.
If Nestlé plays tit for tat but Mars plays always cheat, Nestlé makes a profit of only $150 million in the first year but $160 million per year thereafter.
If Nestlé plays always cheat and Mars does the same, both firms will make a profit of $160 million each year.
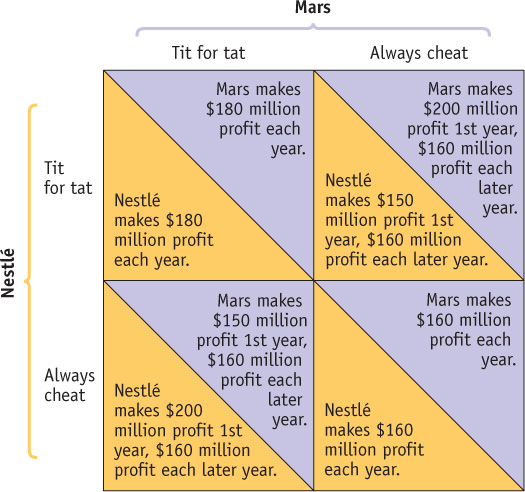
Which strategy is better? In the first year, Nestlé does better playing always cheat, whatever its rival’s strategy: it assures itself that it will get either $200 million or $160 million (which of the two payoffs it actually receives depends on whether Mars plays tit for tat or always cheat). This is better than what it would get in the first year if it played tit for tat: either $180 million or $150 million. But by the second year, a strategy of always cheat gains Nestlé only $160 million per year for the second and all subsequent years, regardless of Mars’s actions.
PRISONERS OF THE ARMS RACE

Between World War II and the late 1980s, the United States and its allies were locked in a seemingly endless struggle with the Soviet Union that never broke out into open war. During this Cold War, both sides spent huge sums on arms, sums that were a significant drain on the U.S. economy and eventually proved a crippling burden for the Soviet Union, whose underlying economic base was much weaker. Yet neither side was ever able to achieve a decisive military advantage.
As many people pointed out, both sides would have been better off if they had both spent less on arms. Yet the arms race continued for 40 years.
Why? As political scientists were quick to notice, one way to explain the arms race was to suppose that the two sides were locked in a classic prisoners’ dilemma. Each government would have liked to achieve decisive military superiority, and each feared military inferiority. But both would have preferred a stalemate with low military spending to one with high spending. However, each government rationally chose to engage in high spending. If its rival did not spend heavily, its own high spending would lead to military superiority; not spending heavily would lead to inferiority if the other government continued its arms buildup. Thus, both governments have the incentive to spend heavily on military because this is their best strategy regardless of the other government’s action. The countries were trapped in an inferior outcome.
The answer to this trap could have been an agreement not to spend as much; indeed, the two sides tried repeatedly to negotiate limits on some kinds of weapons. But these agreements weren’t very effective. In the end the issue was resolved as heavy military spending hastened the collapse of the Soviet Union in 1991.
Unfortunately, the logic of an arms race has not disappeared. A nuclear arms race has developed between Pakistan and India, neighbouring countries with a history of mutual antagonism. In 1998 the two countries confirmed the unrelenting logic of the prisoners’ dilemma: both publicly tested their nuclear weapons in a tit-for-tat sequence, each seeking to prove to the other that it could inflict just as much damage as its rival.
Over time, the total amount gained by Nestlé by playing always cheat is less than the amount it would gain by playing tit for tat: for the second and all subsequent years, it would never get any less than $160 million and would get as much as $180 million if Mars played tit for tat as well. Which strategy, always cheat or tit for tat, is more profitable depends on two things: how many years Nestlé expects to play the game and what strategy its rival follows.
If Nestlé expects the chocolate business to end in the near future, it is in effect playing a one-shot game. So it might as well cheat and grab what it can. Even if Nestlé expects to remain in the chocolate business for many years (therefore to find itself repeatedly playing this game with Mars) and, for some reason, expects Mars always to cheat, it should also always cheat. That is, Nestlé should follow the old rule “Do unto others before they do unto you.”
But if Nestlé expects to be in the business for a long time and thinks Mars is likely to play tit for tat, it will make more profits over the long run by playing tit for tat, too. It could have made some extra short-term profits by cheating at the beginning, but this would provoke Mars into cheating, too, and would, in the end, mean lower profits.
The lesson of this story is that when oligopolists expect to compete with one another over an extended period of time, each individual firm will often conclude that it is in its own best interest to be helpful to the other firms in the industry. So it will restrict its output in a way that raises the profits of the other firms, expecting them to return the favour. Despite the fact that firms have no way of making an enforceable cooperative agreement to limit output and raise prices (and are in legal jeopardy if they even discuss prices), they manage to act “as if” they had such an agreement. When this happens, we say that firms engage in tacit collusion.
When firms limit production and raise prices in a way that raises one another’s profits, even though they have not made any formal cooperative agreement, they are engaged in tacit collusion.
THE RISE AND FALL AND RISE OF OPEC

Call it the cartel that does not need to meet in secret. The Organization of Petroleum Exporting Countries, usually referred to as OPEC, includes 12 national governments (Algeria, Angola, Ecuador, Iran, Iraq, Kuwait, Libya, Nigeria, Qatar, Saudi Arabia, the United Arab Emirates, and Venezuela), and it controls 40% of the world’s oil exports and 80% of its proven reserves. Two other oil-exporting countries, Norway and Mexico, are not formally part of the cartel but act as if they were. (Russia, also an important oil exporter, has not yet become part of the club.) Unlike corporations, which are often legally prohibited by governments from reaching agreements about production and prices, national governments can talk about whatever they feel like. OPEC members routinely meet to try to set targets for production.
These nations are not particularly friendly with one another. Indeed, OPEC members Iraq and Iran fought a spectacularly bloody war with each other in the 1980s. And, in 1990, Iraq invaded another member, Kuwait. (A mainly non-OPEC force based in yet another OPEC member, Saudi Arabia, drove the Iraqis out of Kuwait.)
Yet the members of OPEC, whether they like one another or not, are effectively players in a game with repeated interactions. In any given year it is in their combined interest to keep output low and prices high. But it is also in the interest of any one producer to cheat and produce more than the agreed-upon quota—unless that producer believes that its actions will bring future retaliation.
So how successful is the cartel? Well, it’s had its ups and downs. Analysts have estimated that of 12 announced quota reductions, OPEC was able to successfully defend its price floor 80% of the time.
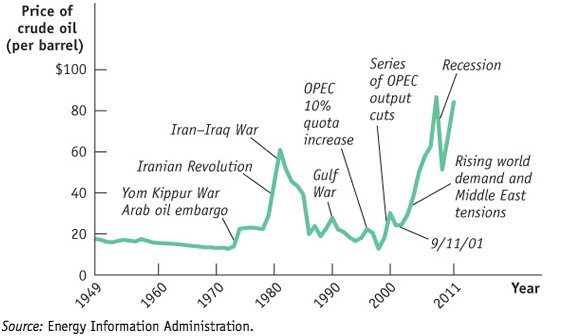
Figure 14-5 shows the price of oil in constant dollars (that is, the value of a barrel of oil in terms of other goods) since 1949. OPEC first demonstrated its muscle in 1974: in the aftermath of a war in the Middle East, several OPEC producers limited their output—and they liked the results so much that they decided to continue the practice. Following a second wave of turmoil in the aftermath of Iran’s 1979 revolution, prices shot still higher.
By the mid-1980s, however, there was a growing glut of oil on world markets, and cheating by cash-short OPEC members became widespread. The result, in 1985, was that producers who had tried to play by the rules—especially Saudi Arabia, the largest producer—got fed up, and collusion collapsed.
The cartel began to act effectively again at the end of the 1990s, thanks largely to the efforts of Mexico’s oil minister to orchestrate output reductions. The cartel’s actions helped raise the price of oil from less than $10 a barrel in 1998 to a range of $20 to $30 a barrel in 2003.
Since 2008, OPEC has experienced the steepest roller-coaster ride of oil prices in its history. By 2008, prices had soared to over $145 a barrel. But at the end of 2008, one year into the Great Recession of 2007–2009, the price dropped sharply to $32 a barrel. In response, producers committed to reduce their output by about 5% of global output, with Saudi Arabia, the world’s largest exporter, leading with cuts of 20% of its output. By early 2009, prices had begun to rebound. Most recently, OPEC has struggled to contain its success. In 2011 political turmoil in several Middle Eastern countries caused prices to skyrocket again. With other producers unwilling or unable to increase their production, in June 2011 Saudi Arabia increased its output in order to prevent shortages in the global oil market.

Quick Review
Economists use game theory to study firms’ behaviour when there is interdependence between their payoffs. The game can be represented with a payoff matrix. Depending on the payoffs, a player may or may not have a dominant strategy.
When each firm has an incentive to cheat, but both are worse off if both cheat, the situation is known as a prisoners’ dilemma.
Players who don’t take their interdependence into account arrive at a Nash equilibrium. But if a game is played repeatedly, players may engage in strategic behaviour, sacrificing short-run profit to influence future behaviour.
In repeated prisoners’ dilemma games, tit for tat is often a good strategy, leading to successful tacit collusion.
Check Your Understanding 14-3
CHECK YOUR UNDERSTANDING 14-3
Question 14.4
Find the Nash equilibrium actions for the following payoff matrix. Which actions maximize the total payoff of Nikita and Margaret? Why is it unlikely that they will choose those actions without some communication?
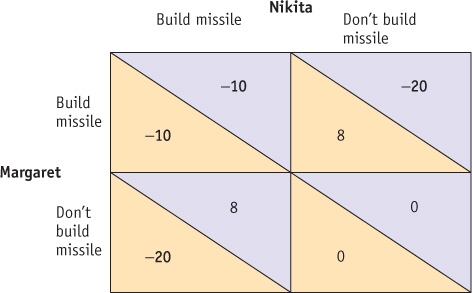
When Margaret builds a missile, Nikita’s payoff from building a missile as well is −10; it is −20 if he does not. The same set of payoffs holds for Margaret when Nikita builds a missile: her payoff is −10 if she builds one as well, −20 if she does not. So it is a Nash equilibrium for both Margaret and Nikita to build missiles, and their total payoff is (−10) + (−10) = −20. But their total payoff is greatest when neither builds a missile: their total payoff is 0 + 0 = 0. But this outcome—the cooperative outcome—is unlikely. If Margaret builds a missile but Nikita does not, Margaret gets a payoff of +8, rather than the 0 she gets if she doesn’t build a missile. So Margaret is better off if she builds a missile but Nikita doesn’t. Similarly, Nikita is better off if he builds a missile but Margaret doesn’t: he gets a payoff of +8, rather than the 0 he gets if he doesn’t build a missile. So both players have an incentive to build a missile. Both will build a missile, and each gets a payoff of −10. So unless Nikita and Margaret are able to communicate in some way to enforce cooperation, they will act in their own individual interests and each will build a missile.
Question 14.5
Which of the following factors make it more likely that oligopolists will play noncooperatively? Which make it more likely that they will engage in tacit collusion? Explain.
Each oligopolist expects several new firms to enter the market in the future.
It is very difficult for a firm to detect whether another firm has raised output.
The firms have coexisted while maintaining high prices for a long time.
Future entry by several new firms will increase competition and drive down industry profits. As a result, there is less future profit to protect by behaving cooperatively today. So each oligopolist is more likely to behave noncooperatively today.
When it is very difficult for a firm to detect if another firm has raised output, then it is very difficult to enforce cooperation by playing tit for tat. So it is more likely that a firm will behave noncooperatively.
When firms have coexisted while maintaining high prices for a long time, each expects cooperation to continue. So the value of behaving cooperatively today is high, and it is likely that firms will engage in tacit collusion.