20.6 PROBLEMS

Question 20.11

For each of the following situations, calculate the expected value.

  1. Tanisha owns one share of RBC stock, which is currently trading at $80. There is a 50% chance that the share price will rise to $100 and a 50% chance that it will fall to $70. What is the expected value of the future share price?

  2. Sharon buys a ticket in a small lottery. There is a probability of 0.7 that she will win nothing, of 0.2 that she will win $10, and of 0.1 that she will win $50. What is the expected value of Sharon’s winnings?

  3. Aaron is a farmer whose rice crop depends on the weather. If the weather is favourable, he will make a profit of $100. If the weather is unfavourable, he will make a profit of –$20 (that is, he will lose money). The weather forecast reports that the probability of weather being favourable is 0.9 and the probability of weather being unfavourable is 0.1. What is the expected value of Aaron’s profit?

Question 20.12

Vicky N. Vestor is considering investing some of her money in a startup company. She currently has income of $4000, and she is considering investing $2000 of that in the company. There is a 0.5 probability that the company will succeed and will pay out $8000 to Vicky (her original investment of $2000 plus $6000 of the company’s profits). And there is a 0.5 probability that the company will fail and Vicky will get nothing (and lose her investment). The accompanying table illustrates Vicky’s utility function.

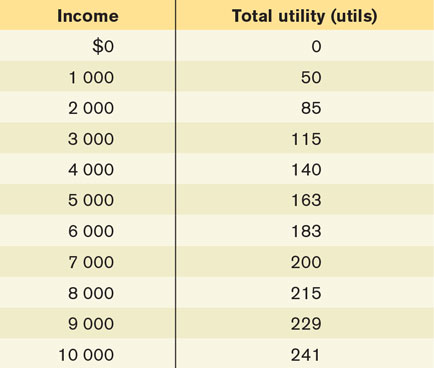
  1. Calculate Vicky’s marginal utility of income for each income level. Is Vicky risk-averse?

  2. Calculate the expected value of Vicky’s income if she makes this investment.

  3. Calculate Vicky’s expected utility from making the investment.

  4. What is Vicky’s utility from not making the investment? Will Vicky therefore invest in the company?

  5. Suppose instead Vicky’s utility function is given by, U(x) = x, where x is her level of income. Repeat parts (a), (c), and (d). (Hint: The slope of the utility function is the change in utility divided by the change in x: 1.)

  6. Suppose instead Vicky’s utility function is given by 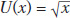, where x is her level of income (i.e., a square root function of her income). Repeat parts (a), (c), and (d). (Hint: The slope of the utility function is the change in utility divided by the change in x:
    0.5 divided by .)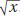

Question 20.13

Vicky N. Vestor’s utility function was given in the table in Problem 2. As in Problem 2, Vicky currently has income of $4000. She is considering investing in a startup company, but the investment now costs $4000 to make. If the company fails, Vicky will get nothing from the company. But if the company succeeds, she will get $10 000 from the company (her original investment of $4000 plus $6000 of the company’s profits). Each event has a 0.5 probability of occurring. Will Vicky invest in the company?

Question 20.14

You have $1000 that you can invest. If you buy Rogers stock, you face the following returns and probabilities from holding the stock for one year: with a probability of 0.2 you will get $1500; with a probability of 0.4 you will get $1100; and with a probability of 0.4 you will get $900. If you put the money into the bank, in one year’s time you will get $1100 for certain.

  1. What is the expected value of your earnings from investing in Rogers stock?

  2. Suppose you are risk-averse. Can we say for sure whether you will invest in Rogers stock or put your money into the bank?

Question 20.15

You have $1000 that you can invest. If you buy Imperial Oil stock, then, in one year’s time, with a probability of 0.4 you will get $1600; with a probability of 0.4 you will get $1100; and with a probability of 0.2 you will get $800. If you put the money into the bank, in one year’s time you will get $1100 for certain.

  1. What is the expected value of your earnings from investing in Imperial Oil stock?

  2. Suppose you prefer putting your money into the bank to investing it in Imperial Oil stock. What does that tell us about your attitude to risk?

Question 20.16

Wilbur is an airline pilot who currently has income of $60 000. If he gets sick and loses his flight medical certificate, he loses his job and has only $10 000 income. His probability of staying healthy is 0.6, and his probability of getting sick is 0.4. Wilbur’s utility function is given in the accompanying table.

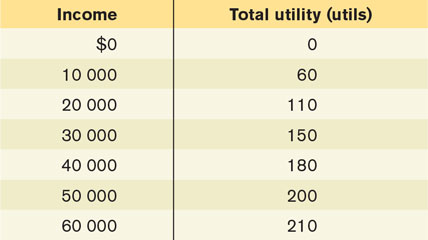
  1. What is the expected value of Wilbur’s income?

  2. What is Wilbur’s expected utility?

    Wilbur thinks about buying “loss-of-licence” insurance that will compensate him if he loses his flight medical certificate.

  3. One insurance company offers Wilbur full compensation for his income loss (that is, the insurance company pays Wilbur $50 000 if he loses his flight medical certificate), and it charges a premium of $40 000. That is, regardless of whether he loses his flight medical certificate, Wilbur’s income after insurance will be $20 000. What is Wilbur’s utility? Will he buy the insurance?

  4. What is the highest premium Wilbur would just be willing to pay for full insurance (insurance that completely compensates him for the income loss)?

  5. Suppose instead Wilbur’s utility function is given by U(x) = ln x, where ln refers to the natural logarithm function on most scientific calculators and x refers to Wilbur’s level of income. Repeat parts (b), (c), and (d).

Question 20.17

In 2012, 1 in approximately every 390 cars in Canada was stolen. Beth owns a car worth $20 000 and is considering purchasing an insurance policy to protect herself from car theft. For the following questions, assume that the chance of car theft is the same in all regions and across all car models.

  1. What should the premium for a fair insurance policy have been in 2008 for a policy that replaces Beth’s car if it is stolen?

  2. Suppose an insurance company charges 0.6% of the car’s value for a policy that pays for replacing a stolen car. How much will the policy cost Beth?

  3. Will Beth purchase the insurance in part (b) if she is risk-neutral?

  4. Discuss a possible moral hazard problem facing Beth’s insurance company if she purchases the insurance.

Question 20.18

Hugh’s income is currently $5000. His utility function is shown in the accompanying table.

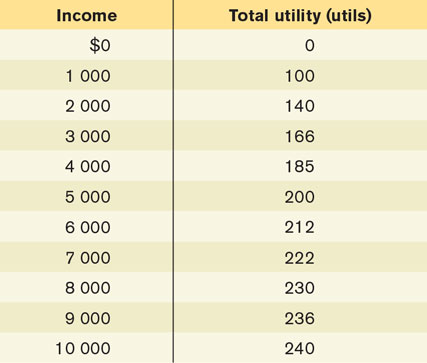
  1. Calculate Hugh’s marginal utility of income. What is his attitude toward risk?

  2. Hugh is thinking about gambling in a casino. With a probability of 0.5 he will lose $3000, and with a probability of 0.5 he will win $5000. What is the expected value of Hugh’s income? What is Hugh’s expected utility? Will he decide to gamble? (Suppose that he gets no extra utility from going to the casino.)

  3. Suppose that the “spread” (how much he can win versus how much he can lose) of the gamble narrows, so that with a probability of 0.5 Hugh will lose $1000, and with a probability of 0.5 he will win $3000. What is the expected value of Hugh’s income? What is his expected utility? Is this gamble better for him than the gamble in part (b)? Will he decide to gamble?

Question 20.19

Eva is risk-averse. Currently she has $50 000 to invest. She faces the following choice: she can invest in the stock of a dot-com company, or she can invest in Telus stock. If she invests in the dot-com company, then with probability 0.5 she will lose $30 000, but with probability 0.5 she will gain $50 000. If she invests in Telus stock, then with probability 0.5 she will lose only $10 000, but with probability 0.5 she will gain only $30 000. Can you tell which investment she will prefer to make?

Question 20.20

Suppose you have $1000 that you can invest in Ted and Larry’s Ice Cream Parlour and/or Ethel’s House of Cocoa. The price of a share of stock in either company is $100. The fortunes of each company are closely linked to the weather. When it is warm, the value of Ted and Larry’s stock rises to $150 but the value of Ethel’s stock falls to $60. When it is cold, the value of Ethel’s stock rises to $150 but the value of Ted and Larry’s stock falls to $60. There is an equal chance of the weather being warm or cold.

  1. If you invest all your money in Ted and Larry’s, what is your expected stock value? What if you invest all your money in Ethel’s?

  2. Suppose you diversify and invest half of your $1000 in each company. How much will your total stock be worth if the weather is warm? What if it is cold?

  3. Suppose you are risk-averse. Would you prefer to put all your money in Ted and Larry’s, as in part (a)? Or would you prefer to diversify, as in part (b)? Explain your reasoning.

Question 20.21

Canadian Bond and New Canadian are two portfolios constructed and managed by Mawer Investment Management Ltd. of Calgary. They comprise bonds and debentures (bond-like securities) of Canadian government and corporate issuers and stocks of smaller Canadian companies. The accompanying table shows the expected value of the annual percentage returns associated with these portfolios based on returns from the period 2004 to 2014.

  1. Which portfolio would a risk-neutral investor prefer?

  2. Jing, a risk-averse investor, chooses to invest in the Canadian Bond portfolio. What can be inferred about the risk of the two portfolios from Jing’s choice of investment? Based on the information in the table, would a risk-neutral investor ever choose Canadian Bond?

  3. Jing is aware that diversification can reduce risk. She considers a portfolio in which half her investment is in units of the Canadian Bond fund and the other half in New Canadian fund units. What is the expected value of the return for this combined portfolio? Would you expect this combined portfolio to be more risky or less risky than the New Canadian fund portfolio? Why?

Question 20.22

You are considering buying a second-hand Volkswagen. From reading car magazines, you know that half of all Volkswagens have problems of some kind (they are “lemons”) and the other half run just fine (they are “plums”). If you knew that you were getting a plum, you would be willing to pay $10 000 for it: this is how much a plum is worth to you. You would also be willing to buy a lemon, but only if its price was no more than $4000: this is how much a lemon is worth to you. And someone who owns a plum would be willing to sell it at any price above $8000. Someone who owns a lemon would be willing to sell it for any price above $2000.

  1. For now, suppose that you can immediately tell whether the car that you are being offered is a lemon or a plum. Suppose someone offers you a plum. Will there be trade?

    Now suppose that the seller has private information about the car she is selling: the seller knows whether she has a lemon or a plum. But when the seller offers you a Volkswagen, you do not know whether it is a lemon or a plum. So this is a situation of adverse selection.

  2. Since you do not know whether you are being offered a plum or a lemon, you base your decision on the expected value to you of a Volkswagen, assuming you are just as likely to buy a lemon as a plum. Calculate this expected value.

  3. Suppose, from driving the car, the seller knows she has a plum. However, you don’t know whether this particular car is a lemon or a plum, so the most you are willing to pay is your expected value. Will there be trade?

Question 20.23

You own a company that produces chairs, and you are thinking about hiring one more employee. Each chair produced gives you revenue of $10. There are two potential employees, Fred Ast and Sylvia Low. Fred is a fast worker who produces ten chairs per day, creating revenue for you of $100. Fred knows that he is fast and so will work for you only if you pay him more than $80 per day. Sylvia is a slow worker who produces only five chairs per day, creating revenue for you of $50. Sylvia knows that she is slow and so will work for you if you pay her more than $40 per day. Although Sylvia knows she is slow and Fred knows he is fast, you do not know who is fast and who is slow. So this is a situation of adverse selection.

  1. Since you do not know which type of worker you will get, you think about what the expected value of your revenue will be if you hire one of the two. What is that expected value?

  2. Suppose you offered to pay a daily wage equal to the expected revenue you calculated in part (a). Whom would you be able to hire: Fred, or Sylvia, or both, or neither?

  3. If you know whether a worker is fast or slow, which one would you prefer to hire and why? Can you devise a compensation scheme to guarantee that you employ only the type of worker you prefer?

Question 20.24

For each of the following situations, do the following: first describe whether it is a situation of moral hazard or of adverse selection. Then explain what inefficiency can arise from this situation and explain how the proposed solution reduces the inefficiency.

  1. When you buy a second-hand car, you do not know whether it is a lemon (low quality) or a plum (high quality), but the seller knows. A solution is for sellers to offer a warranty with the car that pays for repair costs.

  2. Some people are prone to see dentists unnecessarily for minor complaints, and health maintenance organizations do not know how urgently you need a dentist. A solution is for insurees to have to make a co-payment of a certain dollar amount (for example, $10) each time they visit a health care provider. All insurees are risk-averse.

  3. When airlines sell tickets, they do not know whether a buyer is a business traveller (who is willing to pay a lot for a seat) or a leisure traveller (who has a low willingness to pay). A solution for a profit-maximizing airline is to offer an expensive ticket that is very flexible (it allows date and route changes) and a cheap ticket that is very inflexible (it has to be booked in advance and cannot be changed).

  4. A company does not know whether workers on an assembly line work hard or whether they slack off. A solution is to pay the workers “piece rates,” that is, pay them according to how much they have produced each day. All workers are risk-averse, but the company is risk-neutral.

  5. When making a decision about hiring you, prospective employers do not know whether you are a productive or unproductive worker. A solution is for productive workers to provide potential employers with references from previous employers.

Question 20.25

Kory owns a house that is worth $300 000. If the house burns down, she loses all $300 000. If the house does not burn down, she loses nothing. Her house burns down with a probability of 0.02. Kory is risk-averse.

  1. What would a fair insurance policy cost?

  2. Suppose an insurance company offers to insure her fully against the loss from the house burning down, at a premium of $1500. Can you say for sure whether Kory will or will not take the insurance?

  3. Suppose an insurance company offers to insure her fully against the loss from the house burning down, at a premium of $6000. Can you say for sure whether Kory will or will not take the insurance?

  4. Suppose that an insurance company offers to insure her fully against the loss from the house burning down, at a premium of $9000. Can you say for sure whether Kory will or will not take the insurance?