9.7 PROBLEMS
Question 9.14
Hiro owns and operates a small business that provides economic consulting services. During the year he spends $57 000 on travel to clients and other expenses. In addition, he owns a computer that he uses for business. If he didn’t use the computer, he could sell it and earn yearly interest of $100 on the money created through this sale. Hiro’s total revenue for the year is $100 000. Instead of working as a consultant for the year, he could teach economics at a small local college and make a salary of $50 000.
What is Hiro’s accounting profit?
What is Hiro’s economic profit?
Should Hiro continue working as a consultant, or should he teach economics instead?
Question 9.15
Jackie owns and operates a web-
design business. To keep up with new technology, she spends $5000 per year upgrading her computer equipment. She runs the business out of a room in her home. If she didn’t use the room as her business office, she could rent it out for $2000 per year. Jackie knows that if she didn’t run her own business, she could return to her previous job at a large software company that would pay her a salary of $60 000 per year. Jackie has no other expenses. How much total revenue does Jackie need to make in order to break even in the eyes of her accountant? That is, how much total revenue would give Jackie an accounting profit of just zero?
How much total revenue does Jackie need to make in order for her to want to remain self-
employed? That is, how much total revenue would give Jackie an economic profit of just zero? If Jackie earns a negative economic profit but decides to remain self-
employed, is her behaviour irrational? Explain why or why not.
Question 9.16
You own and operate a bike store. Each year, you receive revenue of $200 000 from your bike sales, and it costs you $100 000 to obtain the bikes. In addition, you pay $20 000 for electricity, taxes, and other expenses per year. Instead of running the bike store, you could become an accountant and receive a yearly salary of $40 000. A large clothing retail chain wants to expand and offers to rent the store from you for $50 000 per year. How do you explain to your friends that despite making a profit, it is too costly for you to continue running your store?
Question 9.17
Suppose you have just paid a nonrefundable fee of $1000 for your meal plan for this academic term. This allows you to eat dinner in the cafeteria every evening.
You are offered a part-
time job in a restaurant where you can eat for free each evening. Your parents say that you should eat dinner in the cafeteria anyway, since you have already paid for those meals. Are your parents right? Explain why or why not. You are offered a part-
time job in a different restaurant where, rather than being able to eat for free, you receive only a large discount on your meals. Each meal there will cost you $2; if you eat there each evening this semester, it will add up to $200. Your roommate says that you should eat in the restaurant since it costs less than the $1000 that you paid for the meal plan. Is your roommate right? Explain why or why not.
Question 9.18
New Brunswick, Ontario, and Quebec are the only provinces that have nuclear power plants. Recently, the nuclear plant at Darlington, Ontario, which was completed in 1993 at a price of $14.4 billion, was due for repairs to extend its useful life. According to estimates by Ontario’s Ministry of Energy, the repair cost of the plant could run from $6 billion to $10 billion. At the same time, the cost of building a new nuclear plant in Ontario could range from $10 billion to $20 billion, depending on its size. Is repairing the Darlington plant the right economic decision? Explain.
Question 9.19
You have bought a $10 ticket in advance for a lacrosse game, a ticket that cannot be resold. You know that going to the lacrosse game will give you a benefit equal to $20. After you have bought the ticket, you hear that there will be a CFL football game at the same time. Tickets to the football game cost $20, and you know that going to the football game will give you a benefit equal to $35. You tell your friends the following: “If I had known about the football game before buying the ticket to the lacrosse game, I would have gone to the football game instead. But now that I already have the ticket to the lacrosse game, it’s better for me to just go to the lacrosse game.” Are you making the correct decision? Justify your answer by calculating the benefits and costs of your decision.
Question 9.20
Amy, Bill, and Carla all mow lawns for money. Each of them operates a different lawn mower. The accompanying table shows the total cost to Amy, Bill, and Carla of mowing lawns.
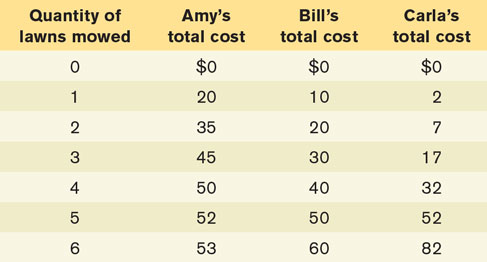
Calculate Amy’s, Bill’s, and Carla’s marginal costs, and draw each of their marginal cost curves.
Who has increasing marginal cost, who has decreasing marginal cost, and who has constant marginal cost?
Question 9.21
You are the manager of a gym, and you have to decide how many customers to admit each hour. Assume that each customer stays exactly one hour. Customers are costly to admit because they inflict wear and tear on the exercise equipment. Moreover, each additional customer generates more wear and tear than the customer before. As a result, the gym faces increasing marginal cost. The accompanying table shows the marginal costs associated with each number of customers per hour.

Suppose that each customer pays $15.25 for a one-
hour workout. Use the profit- maximizing principle of marginal analysis to find the optimal number of customers that you should admit per hour. You increase the price of a one-
hour workout to $16.25. What is the optimal number of customers per hour that you should admit now?
Question 9.22
Georgia and Lauren are economics students who go to a karate class together. Both have to choose how many classes to go to per week. Each class costs $20. The accompanying table shows Georgia’s and Lauren’s estimates of the marginal benefit that each of them gets from each class per week.
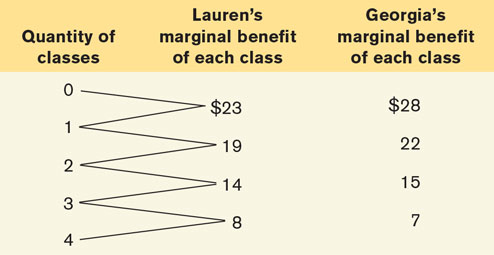
Use marginal analysis to find Lauren’s optimal number of karate classes per week. Explain your answer.
Use marginal analysis to find Georgia’s optimal number of karate classes per week. Explain your answer.
Question 9.23
The Canadian National Advisory Committee on Immunization (NACI) has recommended against vaccinating the whole population against the smallpox virus because the vaccination has undesirable, and sometimes fatal, side effects. Suppose the accompanying table gives the data that are available about the effects of a smallpox vaccination program.
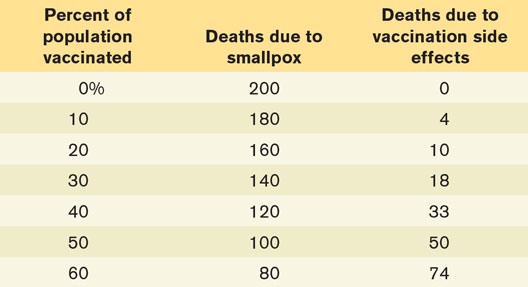
Calculate the marginal benefit (in terms of lives saved) and the marginal cost (in terms of lives lost) of each 10% increment of smallpox vaccination. Calculate the net increase in human lives for each 10% increment in population vaccinated.
Using marginal analysis, determine the optimal percentage of the population that should be vaccinated.
Question 9.24
Patty delivers pizza using her own car, and she is paid according to the number of pizzas she delivers. The accompanying table shows Patty’s total benefit and total cost when she works a specific number of hours.
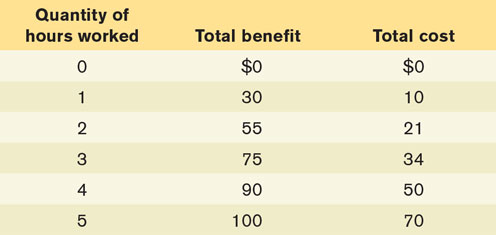
Use marginal analysis to determine Patty’s optimal number of hours worked.
Calculate the total profit to Patty from working 0 hours, 1 hour, 2 hours, and so on. Now suppose Patty chooses to work for 1 hour. Compare her total profit from working for 1 hour with her total profit from working the optimal number of hours. How much would she lose by working for only 1 hour?
Question 9.25
Assume De Beers is the sole producer of diamonds. When it wants to sell more diamonds, it must lower its price in order to induce shoppers to buy more. Furthermore, each additional diamond that is produced costs more than the previous one due to the difficulty of mining for diamonds. De Beers’s total benefit schedule is given in the accompanying table, along with its total cost schedule.
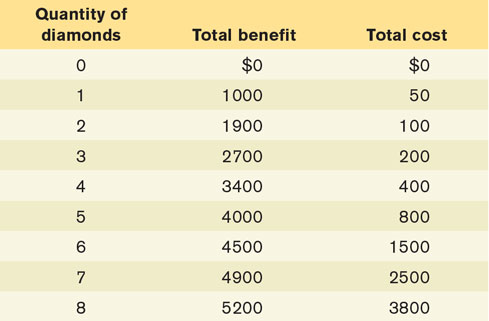
Draw the marginal cost curve and the marginal benefit curve and, from your diagram, graphically derive the optimal quantity of diamonds to produce.
Calculate the total profit to De Beers from producing each quantity of diamonds. Which quantity gives De Beers the highest total profit?
Question 9.26
In each of the following examples, explain whether the decision is rational or irrational. Describe the type of behaviour exhibited.
Kookie’s best friend likes to give her gift cards that Kookie can use at her favourite stores. Kookie, however, often forgets to use the cards or loses them. Kookie, though, is careful with her own cash.
The Western Canada Theatre, in Kamloops, British Columbia, offers Pay-
What- You- Can matinees to ensure everyone can experience live theatre. This payment system allows patrons to pay any amount they like for a seat, instead of the fixed price, although the usual seat prices are publicized as a point of comparison. Rick has just gotten his teaching degree and has two job offers. One job, replacing a teacher who has gone on leave, will last only two years. It is at a private high school, and he will be paid $35 000 per year. He thinks he will probably be able to find another good job in the area after the two years are up but isn’t sure. The other job, also at a high school, pays $25 000 per year and is virtually guaranteed for five years; after those five years, he will be evaluated for a permanent teaching position at the school. About 75% of the teachers who start at the school are hired for permanent positions. Rick takes the five-
year position at $25 000 per year. Kimora has planned a trip to Florida during reading week in February. She has several school projects due after her return. Rather than do them in February, she figures she can take her books with her to Florida and complete her projects there.
Sahir overpaid when buying a used car that has turned out to be a lemon. He could sell it for parts, but instead he lets it sit in his garage and deteriorate.
Barry considers himself an excellent investor in stocks. He selects new stocks by finding ones with characteristics similar to those of his previous winning stocks. He chalks up losing trades to ups and downs in the macroeconomy.
Question 9.27
You have been hired as a consultant by a company to develop the company’s retirement plan, taking into account different types of predictably irrational behaviour commonly displayed by employees. State at least two types of irrational behaviour employees might display with regard to the retirement plan and the steps you would take to forestall such behaviour.