Chapter 3.

Overview

Generality

Although we speak of this model in terms of a mass hanging on a spring oscillating up and down, it actually has extremely wide applicability. The ideas—the constructs, the relationships, and the representations—of this model are used to make sense of the behavior of entities that vibrate ranging from the internal motions of molecules to the internal motions of liquids and solids to macroscopic structures such as a mass hanging on a spring.

This model will play a key role in our development of models of thermal and bond energies of substances in their various physical states.

Focus

Our focus with this introductory model of oscillation is on the energy relationships related to oscillating objects and on the relationship between force and potential energy. There is an emphasis on developing an integrated understanding of the actual visual images of oscillating objects and the various representational tools available in the model. Because this model is fundamentally a more specialized application of the Energy-Interaction Model, it by itself cannot be used to answer questions regarding the time dependence of oscillating systems. Later in the course we will extend this oscillator model to include time dependence, which historically is called simple harmonic motion.

Model Summary

Algebraic Representations

Graphical Representation of Energies of a spring-mass system

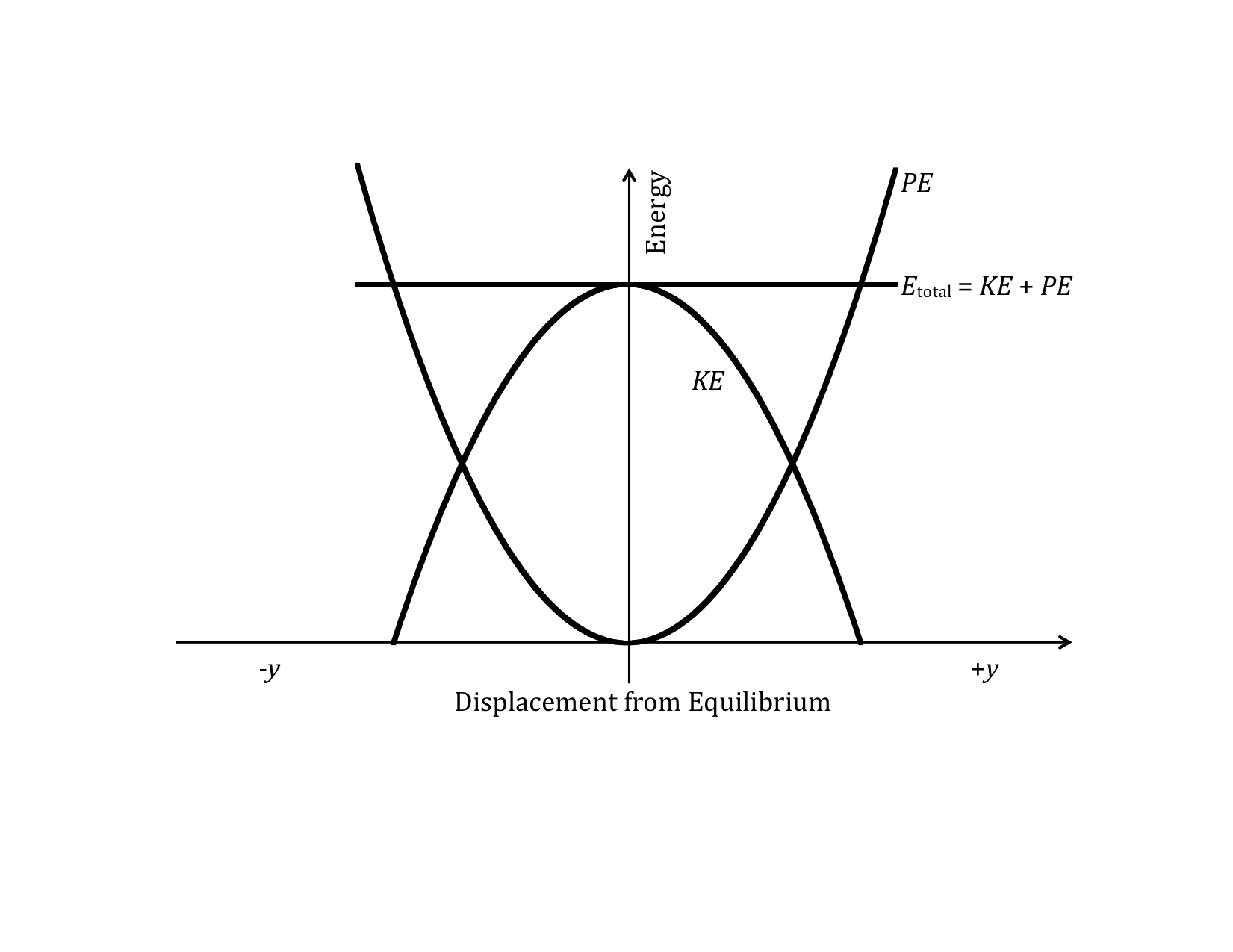
Elaboration

Elastic Object

An object, which when deformed (perhaps by squeezing it or stretching it), returns to its original shape.

Spring

A coiled spiral shaped object that is constructed to be elastic over a large range of deformation. Some springs can only be stretched, but if the coils are initially separated, the spring is elastic when both stretched or compressed.

Spring-mass

A spring with an object whose mass is considerably greater than the mass of the spring attached to one end of the spring.

Hanging spring-mass

A spring-mass with one end solidly attached to a support in a manner that the spring hangs vertically with the mass at the bottom of the spring.

Force

See the expanded definition in the Energy-Interaction Model

Spring force, force constant

Spring force refers to the force with which a spring pulls back when stretched or pushes back when compressed. This force is proportional to the amount of stretch or compression. The force constant is the constant of proportionality, usually written as k.

Spring-mass Force and force constant

A spring with a mass hanging on it acts exactly like a spring without a mass, except that the end of the spring has a different equilibrium position. The spring constant is the same and measurements of the distance the spring is stretched or compressed are made from the new equilibrium position.

Work done on a spring or a spring-mass system by an external agent

When a person stretches or compresses a spring they are doing work on the physical spring system.

Oscillatory motion

An object that behaves like a spring-mass does when the mass is pulled down or pushed up and then released is said to oscillate. The object oscillates about the equilibrium position gradually losing energy to thermal systems until it comes to rest at the equilibrium position.

Energy systems in Oscillatory Motion

If the transfer of energy to thermal systems is negligible an oscillating object behaving like a spring-mass system will move back and forth from one side of the equilibrium position to the other. As it does so, energy is transferred back and forth from the potential energy system to the kinetic energy system. The total energy of the oscillating system is the sum of the potential and kinetic energies and gradually decreases to zero as energy is transferred to thermal systems.

Relationship 1

A spring is an example of an elastic object that has the property that if compressed by some external object (perhaps your fingers) and then the force from the external object is removed, the elastic object returns to its original shape or position. Likewise, if stretched and then released, the elastic object also returns to its original shape or position. It will typically move back and forth when this happens.

The property expressed in this first relationship is truly universal. Almost every object behaves this way if it is not pushed or pulled beyond the point at which the object permanently deforms or cracks. For materials like glass, the maximum amount of compression or force must be kept fairly small, but if it is, a glass behaves the same way a spring does, that is, as an elastic object.

Relationship 2

It is customary to fix one end of the elastic object and then to define the other end of the un-stretched elastic object to be the fixed origin in space (i.e. take the free end to be x=0 or y=0 when the object is un-stretched and call this the “equilibrium” point). The amount of stretch or compression is then measured as the distance from the equilibrium point to the moving end of the elastic object.

For a spring that is fixed at one end it is often convenient to set the origin for measuring the amount of stretch or compression at the location of the free end. If there is a mass attached to the free end of the spring, some point on the mass, such as the top edge, for example, can be used as the point from which to measure the amount of stretch or compression.

Relationship 3

A mass hanging on a stretched spring is an example of an elastic object that we will frequently use.

There are several reasons why we keep coming back to the hanging spring-mass system as the physical example that represents the behavior that all elastic objects exhibit. First, it is easy to directly observe the behavior of a spring-mass and make simple measurements on. Second, it is easy to mentally picture its behavior. Third, the constructs and representations we use to describe the motions of a spring-mass system can be applied to any other elastic object, such as one of carbon atoms in diamond, which is more difficult to visualize. The constructs and mathematical relationships (restoring force, force constant, displacement from equilibrium, energy relationships) we use for an oscillating spring-mass are precisely those we use for the carbon atom in diamond as well as for any other elastic object. It is much easier to develop a deep understanding of these constructs and relationships in the context of a mass hanging on a spring and then transfer them to invisible objects such as atoms, then vice-versa.

Relationship 4

A hanging mass in the earth’s gravitational field acts exactly like a mass attached to a horizontal spring (or a spring-mass in outer space), as long as the equilibrium point is determined when the mass is stationary and hanging on the spring, rather than from the equilibrium point of the spring alone without the mass. That is, the expression for the potential energy, PE _spring-mass , has exactly the same form whether the spring is horizontal or vertical. The earth is not considered to be an external object acting on the spring-mass object, as long as the equilibrium point is determined as just described.

When a mass is hung on the bottom of a vertically hanging spring, the spring stretches a certain amount, but then the mass comes to rest with the spring stretched a certain amount compared to its length prior to attaching the mass. However, the force required to push up or to pull down the mass a certain amount is exactly the same as it is for the spring without the mass. Also, the potential energy change of the spring-mass system when it is stretched on compressed a certain amount is the same as the change in the potential energy of the spring if compressed the same amount without the mass. The key point here, is that we measure the amount of extension or compression from the new equilibrium position with the mass hanging on the spring. Another important point to remember, is that the potential energy of the spring-mass system automatically takes into account the change in potential energy of the spring by itself as well as the change in gravitational potential energy of the mass-earth system. This is why we speak of the spring-mass system, rather than just saying “spring,” and why we write the potential energy of this system as PE_spring-mass.

Relationship 5

A stretched or compressed object (e.g., a spring-mass system) is characterized by an elastic constant or spring constant that is unique to the particular object or spring. Both the force and the PE depend linearly on this constant. The spring constant for a spring is the same whether there is a mass hanging on it or not. (Note: we assume in all this that we don’t permanently deform the elastic object by compressing or stretching it too far.)

The force constant, typically denoted by the symbol “k” depends on the details of the elastic material (aluminum or steel, for example) and for the case of a spring or spring-mass, it depends on the size and shape of the spring and is often referred to as the spring constant. The spring constant is a quantitative measure of the “stiffness” of a spring. A more “springy” spring will have a smaller spring constant, k, then a “stiffer” spring.

Relationship 6

The spring force with which the spring pulls back when stretched or pushes back when compressed is directly proportional to the spring constant and the distance moved from equilibrium.

The force with which a spring pulls back, sometimes referred to as the restoring force, when stretched (or pushes back when compressed) is proportional to the amount of stretch from equilibrium, provided the spring is not stretched too far. (Historically, this linear proportionality between the force and amount of stretch was referred to as Hooke’s law behavior.) We write the force with which the spring pulls or pushes back (the restoring force) as

F = -kx,

where k is the “spring constant” or “force constant” and x is the distance the spring is stretched or compressed from the equilibrium position. The minus sign indicates that the force that the spring exerts is opposite in direction to the direction it was stretched or compressed.

The force that you (an external agent) have to exert on the spring to stretch it a distance x is in the opposite direction to the force the spring exerts (restoring force) and is equal to +kx. The force you exert is in the same direction as the movement of the spring.

When talking about a hanging spring-mass system, often the distance variable is written using a “y” rather than an “x,” which is simply a matter of notation and does not change the meaning of the relationship in any way. We again stress that for a hanging spring-mass system, the distance variable is always measured from the equilibrium (at rest) position after the mass is attached to the spring.

Note on Units: In order for the force to have units of newtons, the units of k must be newtons per meter and the distance x must be expressed in meters.

Relationship 7

The PE of the spring-mass system is directly proportional to the spring constant and the square of the distance moved from the equilibrium position.

W = (average force) × (distance) = F|| y

The expression in the preceding paragraph represents the work I did on the system, so its PE must have increased by that same amount. It doesn’t matter how the spring got stretched (that is, whether it was extended or compressed). If stretched by an amount y, it must have a PE relative to the equilibrium position (with mass attached) of

PE_spring-mass = ½ ky²

The change in the spring-mass potential energy, ∆PE spring-mass can be found using the Energy-Interaction Model in the standard way. Let’s assume in this example that I compress or stretch the spring further from its equilibrium position than when it was in its initial position, y_i, to a final position y_f. Therefore, I am doing positive work on the spring-mass system. That is, I am adding energy to the spring-mass system. (The work I do on the spring-mass system will be a positive number of joules.) Thus, its energy must increase. If I don’t change its KE, i.e., don’t change its velocity (the final velocity is equal to its initial velocity), the only energy system that changes is the PE_spring-mass energy system.

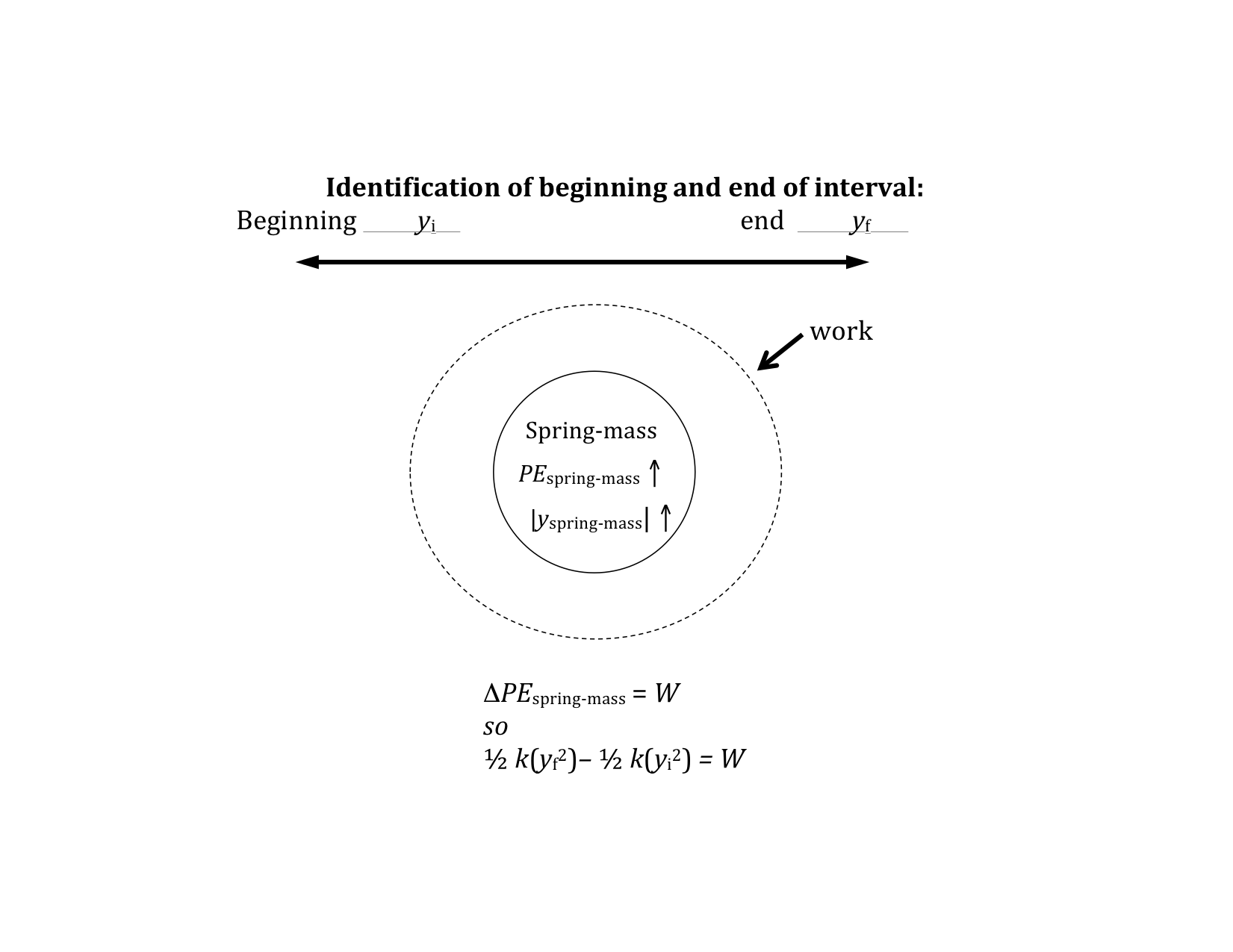
Notice the difference between the equation written in the diagram just above this sentence and the expression for PE spring-mass written above the previous paragraph. These two equations look similar, but they mean entirely different things. The first is simply the value of the PE_spring-mass with the standard convention of putting the origin for measuring the stretch or compression at the equilibrium position. The second is the change in PE_spring-mass as the position changes from the initial position, y_i to the final position, y_f.

Relationship 8

In one dimension the magnitude of the spring force is related to the potential energy by |F| = |d(PE)/dr|. The force is always in the direction that lowers the potential energy. (Note: This is the same as Relation (2) that appears in Intro Particle Model of Matter.)

There is a general relationship between any potential energy and the force that is associated with that potential. This relationship has a useful graphical representation that will help us better understand the spring-mass potential energy and also other potential energies we will encounter in the future.

The figure shows the potential energy of a spring-mass system. Marked on the figure are the positions where the force exerted by the spring has the greatest and the least values. If pulled or pushed to some value of the position y, what do we know about the restoring force of the spring?

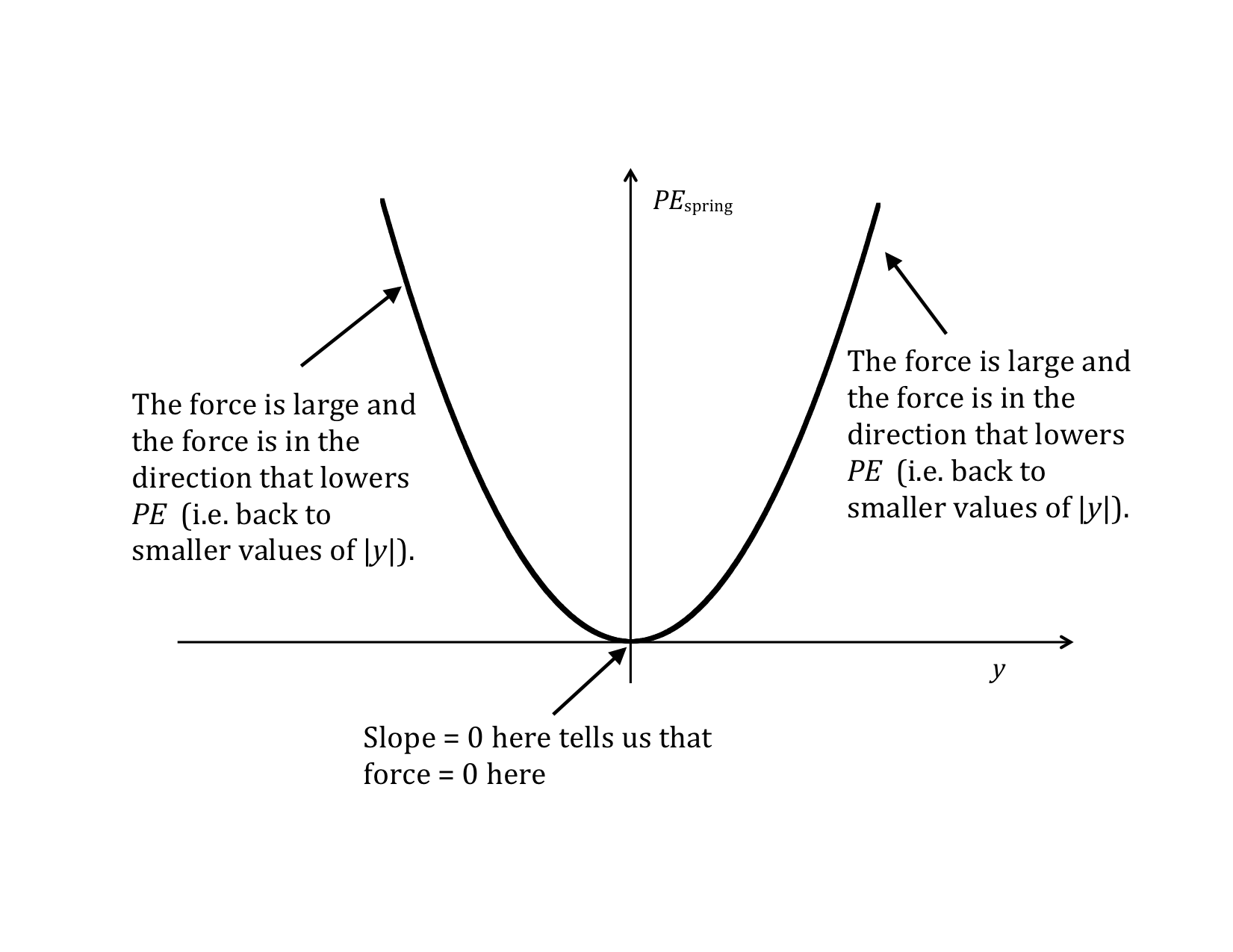
Without derivation, we simply state the result that the force exerted by the spring is equal to the negative of the derivative of the PE with respect to y. Graphically, the force is the negative of the slope of the PE vs. y curve. Rather than worry about the negative sign here, however, we simply focus on the fact that the spring always tries to get back to its equilibrium position. This is what tells us the direction of the force.

For any potential energy that varies in only one spatial dimension, it is true that the magnitude of the force associated with that potential energy is equal to the derivative of the potential energy with respect to the position coordinate associated with the force. Using the symbol r for generality, we can write this symbolically as:

This is a general result that is true for the force associated with any 1-D potential energy. Since the value of the slope gives the magnitude of the derivative of a function, the steeper the slope of a PE curve plotted against its position variable, the greater the magnitude of the force. The restoring force of the spring will be zero when the slope is zero, which occurs at the equilibrium point; i.e., where the object comes to rest when it stops oscillating.

Relationship 9

For an isolated elastic object (e.g., spring-mass system) the energy transfers back and forth between KE and PE. At the extremes of the oscillation PE is a maximum and KE is zero and when the PE is a minimum (when the mass is passing through its equilibrium point) the KE is at its maximum value. The instantaneous values of the spring mass PE and KE add to a constant E_total.

The kinetic energy of the spring-mass system is the same as for any mass that has a speed, v.

where m is the mass of the object hanging on the spring (and part of the mass of the spring itself if it is not negligible compared to the mass of the hanging object) and v is the speed (the rate of change of the position, y) of the mass.

The change in the KE_spring-mass is calculated the same way as the change of any energy:

A mass attached to a spring will oscillate if it is pulled away from its equilibrium position and released. Energy is transferred back and forth between the kinetic energy system of the mass and the potential energy system of the spring. If there were no friction, the oscillation would continue forever, with energy transferring back and forth between the kinetic and potential energy systems.

The maximum value of the PE of this spring-mass system occurs when the mass is at its extreme positions and its speed is zero. Conversely, the KE of the spring-mass system is a maximum when the mass is at its equilibrium position (y = 0). We know from the Energy-Interaction Model that in the absence of friction, ∆E_tot = ∆KE + ∆PE = 0, or in words, E_tot is a constant. Looking at E_tot at any particular time in its cycle of vibration, the energy is still going to be equal to the same total value. Written symbolically, this becomes:

The graph below shows the KE and PE of a spring-mass system as a function of the position from equilibrium. The kinetic energy as a function of y, KE(y), is just the difference between the maximum energy, E_max, and PE(y). This is just another way of expressing conservation of energy for this system. Both PE(y) and KE(y) are parabolas, centered about y = 0. The shape is due to the dependence on the square of y in the expression of the PE.

Although we cannot show it now without investigating the time behavior of the motion of the mass, it turns out that the time-average (that is, the average over time) of the PE and KE are the same, and are consequently both equal to one-half the total energy.

The fact that the time-average potential and kinetic energies are the same has a profound implication for the model of matter. This result is true only for a potential energy that depends on the square of the variable. It is precisely the fact that the potential energy is quadratic with respect to position that makes a spring-mass system so special, so universal, and so important.

The lowest point on the PE(y) curve is frequently called the potential energy minimum. Why is the value of the position variable for which the potential energy is a minimum significant? Consider what happens as energy is removed from a system which is oscillating about the equilibrium value of its position (e.g., a real spring-mass system, because of friction, gradually transfers mechanical energy to thermal energy). The amplitude (maximum extent) of the oscillations decreases until eventually, when all mechanical energy has been transferred to thermal systems, the system comes to rest at the equilibrium position, the position of the potential minimum.

Now consider any physical system that oscillates and which will settle down to a stable position as energy is transferred to thermal systems. That stable equilibrium position represents the physical state where potential energy is smallest. (All of the PE and KE have been transferred to thermal systems.) The potential energy must increase as y increases (either positively or negatively) away from zero, the equilibrium position. Now nature seems to prefer smooth changes of things like potential energies. The simplest smooth mathematical function that increases for both positive and negative y is y². When we look at real physical systems, it turns out that sufficiently close to the minimum, the potential energy always “looks parabolic”! This is a result with far reaching consequences. It implies that any oscillating system behaves just like our simple spring-mass system, at least for small amplitudes of oscillation! What’s important is not that the spring-mass system is so special itself; it is, rather, that the behavior of the spring-mass system represents a truly universal behavior of any oscillating system! We will use this property when we model the real atoms of liquids and solids as “oscillating masses and springs.”