Chapter 1. Astronomical Coordinate Systems

Introduction

The concept of the celestial sphere is a simple but useful model of the sky above us. In this model, the sky is considered to be a vast spherical shell centered on the Earth. All of the objects that appear in the sky are assumed to be so far away that they are equidistant (and infinitely distant) from the Earth on the celestial sphere, rendering the sky as a two-dimensional spherical surface.

The spherical geometry of astronomical coordinate systems is less familiar than the Cartesian coordinate systems used for flat surfaces, but the basic concepts are equivalent. The position of an object on a two-dimensional surface, whether flat or spherical, requires only two coordinates. In a spherical coordinate system, a reference plane is chosen that passes through the center of the sphere and intersects the surface along a great circle, and a particular point on this circle is chosen as a reference point. The first coordinate is defined by the perpendicular arc from the reference plane to the object, measured along the surface of the sphere. The second coordinate is given by the arc along the great circle defined by the reference plane, measured from the reference point to the point perpendicularly below (or above) the object.

One difference between the coordinate system of a flat surface (often referred to as an “X – Y coordinate system”) and that of a spherical surface is the dimensions used in these coordinate axes. In the coordinate system of a flat surface, these dimensions are linear and are measured in units of length. In a spherical coordinate system, these dimensions are angular, equal to the angle subtended at the center of the circle by the arcs described above.

The reference plane and reference point of a coordinate system are chosen to make it convenient for a particular purpose. In this project, you will explore methods for specifying the position of objects in the sky based on several specific reference frames using the model of the celestial sphere.

A. Spherical Geometry

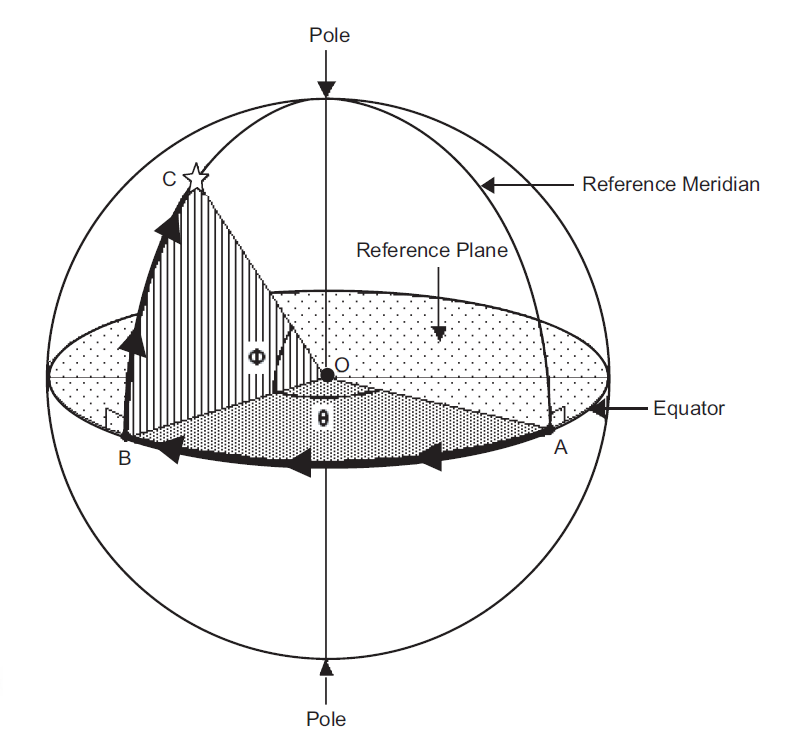
Figure 1 shows the sky modeled as a spherical shell, O being the center of the sphere, as labeled in the figure. Any plane containing O will intersect the sphere on a circle defined as a great circle. One specific great circle is chosen as a reference plane for a spherical coordinate system and is known as the equator, since it divides the sphere into two equal hemispheres.

A line passing through the center of the sphere perpendicular to the reference plane intersects the sphere at two points called poles. Each pole is at the center of its respective hemisphere. Any plane perpendicular to the equator passing through the center of the sphere will include both poles and intersect the sphere in specific great circles known as meridians.

We can select a reference point on the equator, point A in the figure, such that the meridian through A becomes the reference meridian. The position of any object on the sphere, such as the star at point C, can now be specified by two measurements. The first of these is the angular distance of the object from the equator, as measured along the object’s meridian, from point B to point C in the figure. The second is the angular distance along the equator from the reference point A to the meridian passing through the object, point B in the figure.

Note that angular arcs rather than straight lines describe these distances. The angular size of an arc is measured by the angle formed by the radial lines that connect the center of the sphere to each of the endpoints of the arc. Thus, the angular size of the arc AB in the figure is the angle AOB and is labeled θ. Similarly, the angular distance of the star at point C from the equator along the star’s meridian is the angle BOC and is labeled Φ in the figure. Thus, any location on the sphere can be specified uniquely by using these two coordinates, θ and Φ.

A familiar example of a spherical coordinate system is that of latitude and longitude on the surface of the Earth.

The view shows the Earth as seen from space. The viewing location is 12,000 kilometers above the surface of the Earth along a line connecting the center of the Earth and the center of the Sun. The image of the Earth is overlaid with a grid representing the terrestrial spherical coordinate system of latitude and longitude. The equator of the coordinate system is the red line running horizontally across the center of the Earth. The reference plane of the equator is chosen to be perpendicular to the rotation axis of the Earth. In this way, the north and south poles of the coordinate system, indicated by the short blue and yellow lines extending from the top and bottom of the Earth’s surface in the view, coincide with this rotation axis.

Latitude is the angular distance north or south of the equator. The view shows several parallels of latitude, so-called because they are parallel to the equator. Notice that they are labeled in units of degrees, positive to the north of the equator and negative to the south of the equator.

The vertical red line across the surface of the Earth is the reference meridian for longitude. (By standard usage, a meridian of longitude (or a terrestrial meridian) is half of a great circle, and extends from one pole through the equator to the other pole.) This reference meridian, also called the prime meridian, was chosen earlier in history to pass through the site of the Old Royal Observatory at Greenwich, England. Longitude is measured east or west of this prime meridian. The two coordinates of latitude and longitude uniquely specify any location on the surface of the Earth.

You may have noticed that Starry Night™ has labelled the meridians of longitude in units of time (hours), rather than units of angle (degrees). The reason for this is that the Earth rotates once on its axis in 24 hours with reference to the direction to the Sun. Consequently, any location on the Earth moves 360° around a circle oriented parallel to the equator in 1 day of 24 hours. Thus, longitude can also be expressed in units of time: 1 hour of longitude is equal to the angle turned through by the Earth in that time, that is, 360° ÷ 24, or 15°.

As time passes, note that the meridians of longitude move with the Earth as the Earth rotates toward the east. In other words, the coordinate system is fixed on the Earth.