Problem Statement
Assume that . Find sin(θ), sec(θ), and cot(θ) if tan(θ)=
.
Step 1
Recall the signs of sin(θ) and cos(θ) for .
Question Sequence
Question 1
For , sin(θ) and cos(θ) are . Thus we can use the definitions of the trigonometric functions associated with a right triangle to find sin(θ), sec(θ), and cot(θ).
Step 2
Draw a right triangle to find sin(θ) and cos(θ) given that tan(θ)=.
Label θ as one of the acute angles inside the right triangle. Label the leg of the triangle opposite θ as b and label the leg of the triangle adjacent to θ as a. Label the hypotenuse c.
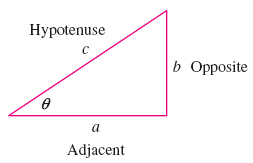
According to this triangle, we can solve for b and a using the relationship
.
Question Sequence
Question 2
Since , we have b = 5 and a = .
Step 3
Knowing that a = 6, b = 5, and c = 7.81, we can solve for sin(θ) and cos(θ) using their definitions with respect to a right triangle.
Question Sequence
Question 4
= .
Step 4
Recall the definitions of sec(θ) and cot(θ).
Question 7
sec(θ) =
cot(θ) =
Step 5
Find and simplify sec(θ) and cot(θ) using, from Step 3, sin(θ) = 0.64 and cos(θ) = 0.77.
Question Sequence
Question 8
For and tan(θ) =
we have
sec(θ) =
(Rounded to two decimal places.)