Problem Statement
Determine a domain on which f−1 exists, and find a formula for f−1 for this domain of f.
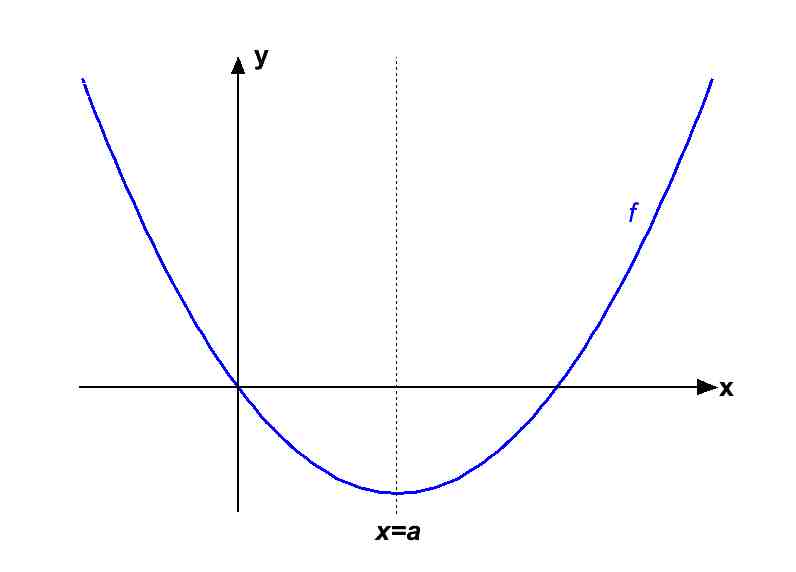
Step 1
Question Sequence
Question 1
The inverse function, f-1(x) exists if and only if f(x).
Step 2
Since f(x) is not one-to-one, it is not invertible. However, we can restrict the domain to one where f(x) is one-to-one and hence f(x) will be invertible on that domain.
Question Sequence
Question 3
Given any parabola, if we restrict the domain to only those numbers to the right (or left) of the vertex, then by the horizontal line test, the function be one-to-one and hence invertible.
Step 3
Now that we have a domain on which f(x) is invertible, let's find a formula for f−1(x). To do so, solve y = f(x) for x in terms of y.
There can only be one inverse function and it depends on the restricted domain of f.
Question Sequence
Question 6
Solve for x in the restricted domain of f, x ≥ 6.
Solve for x in the restricted domain of f, x ≤ 6.
Where a = .