Chapter 1.

1.1 Problem Statement

6
$int/100
round(log(2)/log(1+$r/12),0)

If P0 dollars are deposited in a bank account paying $int % interest compounded monthly, then the account has value after N months. Using a graphing utility, find, to the nearest integer N, the number of months after which the account value doubles.

1.2 Step 1

We need to find the account value after N months that makes the account value equal to double its initial investment value, P0.

Question Sequence

Question 1.1

Thus we need to solve = XvVM00l89Is=·P0.

Incorrect
Correct

Question 1.2

This equation contains the variable N but also the "mystery quantity" P0.

All that we know about P0 is that it must be iPQsYf19/gYNwdn/lyBwUwPcWlnFQlvpR0Wo/q5IDfhdwaezGKzk3JvAm2GQIcTO6AKabW+SZpbZRPGBeggM1A==.

Incorrect
Correct

1.3 Step 2

Question Sequence

Question 1.3

To isolate the factor with N, and because P0 ≠ 0, we may divide each side of the equation by P0.

XvVM00l89Is=

Incorrect
Correct

1.4 Step 3

Question Sequence

Question 1.4

Approximate the solution of graphically.

The figure shows the graphs of and .

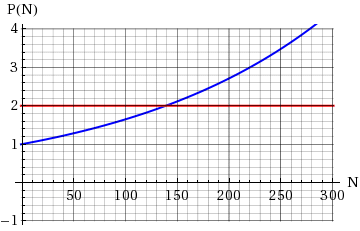
Where the graphs intersect, the initial account value has doubled. At the point of intersection, the number of months N is approximately N = KI9LZTi0ZHOYl6rthTqrw+CKlDxfLDuE4PhPi+VbcSh4TlDJC4pCkRWNAJz+jOqQ.

Incorrect
Correct