Calculus Tutorial 2.2.053
Problem Statement
#Tutorial variables
#per editor, only two points now so that randomization is possible.
do{
($t_sel, $t_les) = pick(2, (4..7) );
@t_c = (1, 1, 3, 3, 5, 5, 6, 6);
}until( $t_c[$t_sel]!=$t_c[$t_les] );
@t_sign = ('-', '+', '-', '+', '-', '+', '-', '+');
@t_answ = (3, 3, '-infinity', 4, 2, -3,'infinity','infinity');
$a=$t_c[$t_sel];
$b=$t_c[$t_les];
$c=$t_sign[$t_sel];
$d=$t_sign[$t_les];
$e=$t_answ[$t_sel];
$f=$t_answ[$t_les];
''
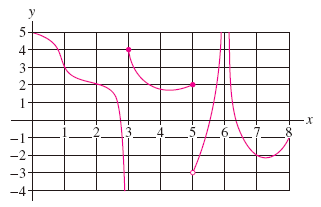
Determine the one-sided limits of the function f(x) in the figure at the points c = 5, 6.
Step 1
Recall how to find one-sided limits.
Question Sequence
Question 1
The limit converges to L as x approaches c through values c.
Incorrect.
Correct.
Step 2
From the graph given in the Problem Statement, determine the left-handed limits by examining the values of the function for values of x slightly less than and approaching the given value c. (enter "inf" for )
Question Sequence
Question 6
2
Correct.
Try again.
Incorrect.
Step 4
To determine the right-hand limits, examine the values of the function for values of x slightly greater than and approaching the given value of c. (enter "inf" for ).
Question Sequence
Question 7
2
Correct.
Try again.
Incorrect.