Chapter 1. RogaCalcET2 2.4.004.Tutorial.SA.

1.1 Problem Statement

Consider the graph of a function g.

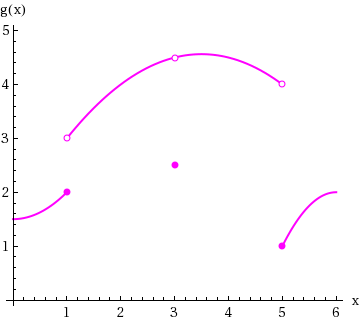
Find the point c at which the function has a jump discontinuity but is left-continuous. What value should be assigned to g(c) to make g right-continuous at x = c?

1.2 Step 1

A function g has a jump discontinuity at x = c if and exist, but are not equal.

Question Sequence

Question 1.1

The graph of g has jump discontinuites at x = 0VV1JcqyBrI= and x = 5.

Incorrect.

Correct.

Question 1.2

There is not a jump discontinuity at x = 3 since nhQwv+c4LNyuPzKZSoVQwGwkLo/Hu0z9NCUGxA==.

Incorrect.

Correct.

1.3 Step 2

A function g is left-continuous at x = c if .

Question Sequence

Since the problem asks for a point on the graph that is both a jump discontinuity and is left-continuous, check x = 1 and x = 5 to determine if the function is left-continuous at either of these values.

Question 1.3

For x = 1: = XvVM00l89Is= and g(1) = XvVM00l89Is=.

For x = 5: = h4XZagboIgc= and g(5) = 0VV1JcqyBrI=.

Correct.

Incorrect.

Question 1.4

Thus, g has a jump discontinuity and is left-continuous at x = 0VV1JcqyBrI=.

Correct.

Incorrect.

1.4 Step 3

A function g is right-continuous at x = c if .

Question 1.5

Since = 607M7xmPORU=, to redefine the given function g to make it right-continuous at x = 1, assign g(1) = 607M7xmPORU=.

Correct.

Incorrect.