Chapter 1. RogaCalcET2 2.4.023.Tutorial.SA.
1.1 Problem Statement
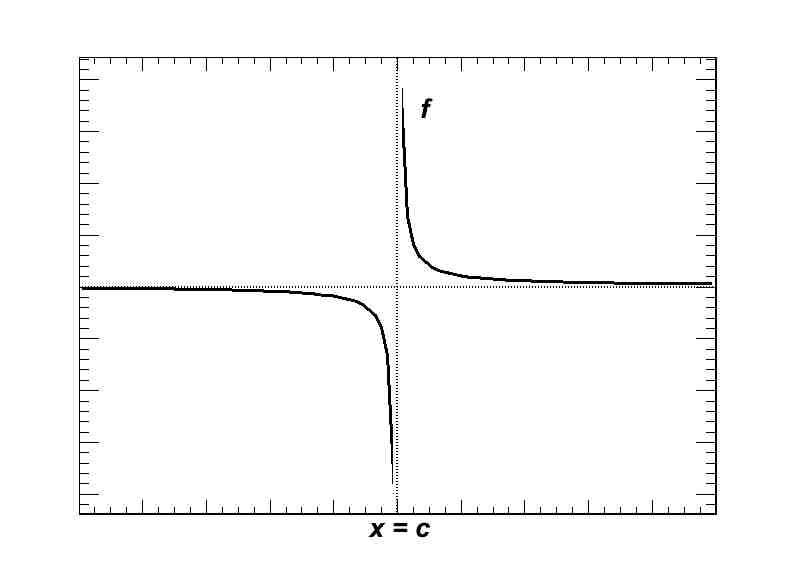
Determine the points of discontinuity. State the type of discontinuity (removable, jump, infinite, or none of these) and whether the function is left- or right-continuous.
1.2 Step 1
Question 1.1
The given function is a XM710SMi641HyNNecqNOfH4LMtA/+uB6FTuzbFDMCSM8K2RI8zMhAA== function and it is continuous 9bNSmg8XLMp82FekXNTzdLcSKM+x6IoldhY6JiT8HszcnOkA4iQuFBtCPKHBFq/uOgkAB4M8XzAUZmbdlvnVsxzdlDKHFILz+T6efMzs2G8=.
1.3 Step 2
Question Sequence
Recall that the domain of a rational function is defined for all values of x except those values for which
.
Question 1.2
Solve for x.
x = ftB1gIsQOozdRQwA/JPVx0k4/R6UPT/F9dFxb7cMfFM=.
Question 1.3
Therefore the domain of is all real numbers except
x =ftB1gIsQOozdRQwA/JPVx0k4/R6UPT/F9dFxb7cMfFM=.
Question 1.4
Because it is a rational function, is continuous over it's domain. Thus,
is discontinuous at the point x = ftB1gIsQOozdRQwA/JPVx0k4/R6UPT/F9dFxb7cMfFM= since this is the value at which f(x) is not defined.
1.4 Step 3
Recall the possible types of discontinuities.
Question Sequence
Question 1.5
If exists but is not equal to
, then x = c is a(n) eHjzXf7gcKm0dLL/5oRTaC348tLf+XHS8ZQobsmQTS4= discontinuity.
Question 1.6
If and
exist but are not equal, then x = c is a(n) Au6BjwX198+Y0xRTH+8NaWPj32E2K1ICN2kVgw== discontinuity.
Question 1.7
If one or both of and
is infinite, then x = c is a(n) 8Zch0aesnQY3cV5BJQoTpBdBoGzhcVMmL27UzU0slrA= discontinuity even if
itself is not defined at x = c.
Question 1.8
To determine the type of discontinuity at , find the one-sided limits as x approaches
.
=ugHNTI1hRxM=
=3LecBr2w/JA=
(Use "inf" for ∞ and "-inf" for -∞)
Question 1.9
eS5qza/T2zjqxFhQ+EaKo9xz/aZtnJFYG0osnPaEQfdxOwKYIarbLG6pJgMly6tqQ0QqyQa+ghaZIqQuOjrVUEoC5PCTseZybt9CGxiW8utdXKjLF7g6/f34Rs3z/Y4s96wCBBtTPjqcH+CCpHX4nLpD5VzbTIqYXm/wixEC6xXLTpEV1D9GIe0Z+8kjIleJTMPCthzgMjEMM3Cf3Sr30GNQW6Qzv0HN19EJNDjtXKpZkBNC7Y7OZnyDHWm17bFdxCRZmXE7Id1nfptFV4NVpHchk6YOlM9+aPTlCH9UUcl2TRIL/ZDlbjYvZ5PJfTe7wX3SAExEv408zQDHB0D3wltVUPzh12mEf7S5fm7+Sz2ecYfk+2CKrOA0qXd8xkCQDc7KrGAQKzdMzqIc1.5 Step 4
Recall the definition of a one-sided continuity at x = c for a given function .
Question 1.10
If , the function is T1QAvMquxITmteCofDF98w==-continuous at x = c.
If , the function is y/8elwqLKvMQPfWtffwxDQ==-continuous at x = c.
Question 1.11
A graph of the function is shown below (c = $b/$a).
