Calculus Tutorial 2.6.006
Problem Statement
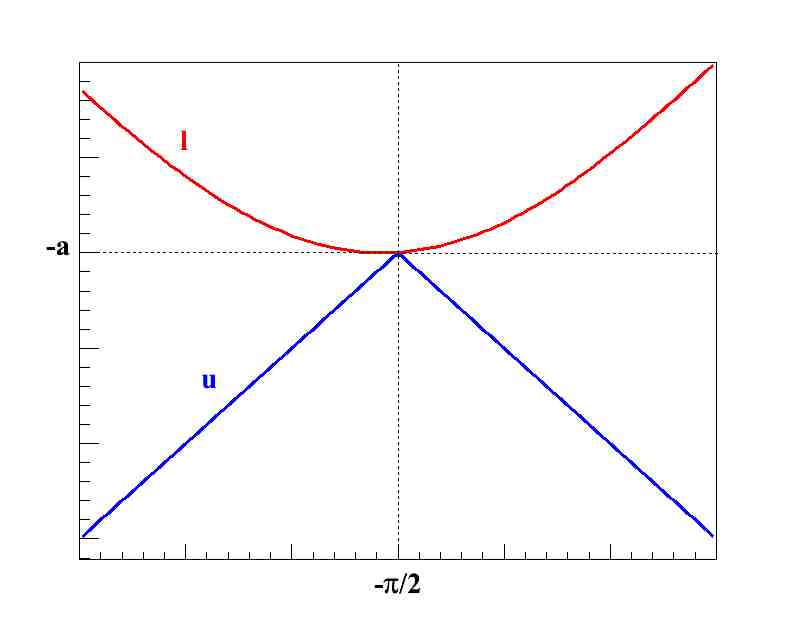
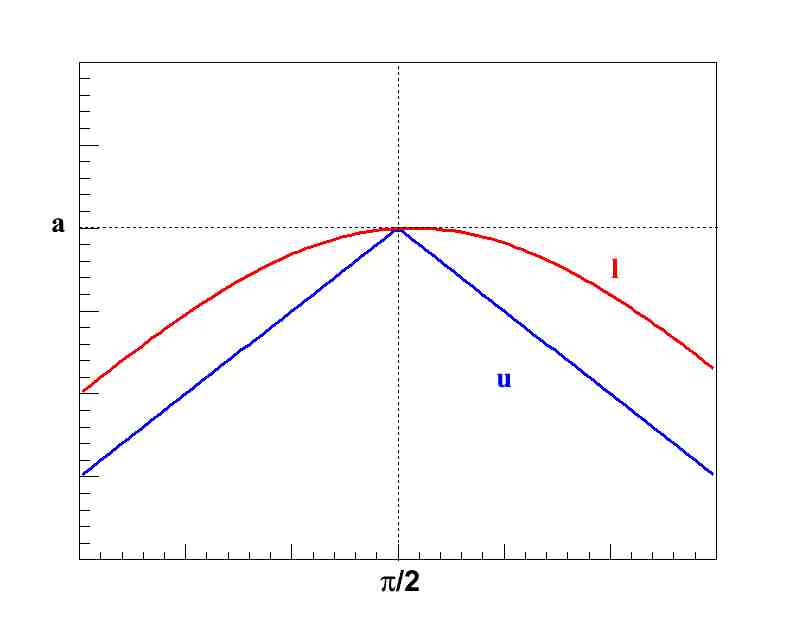
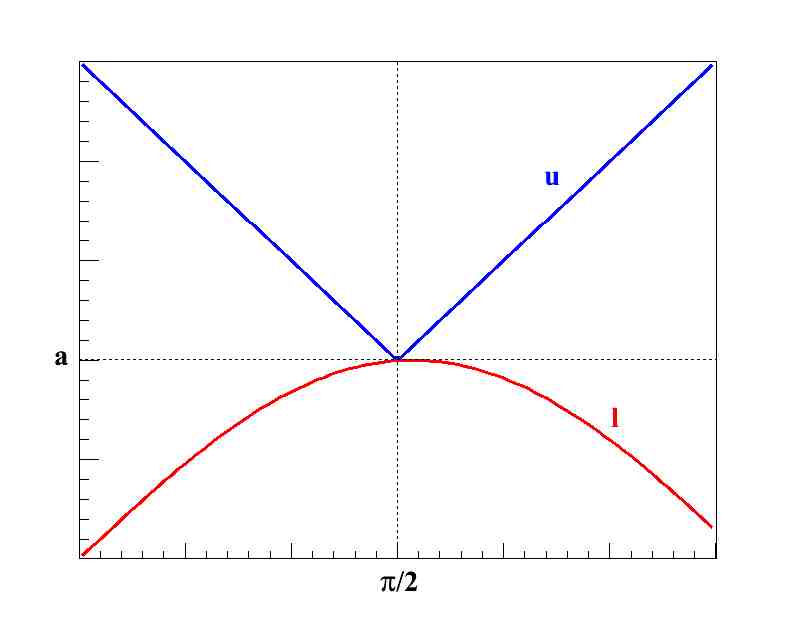
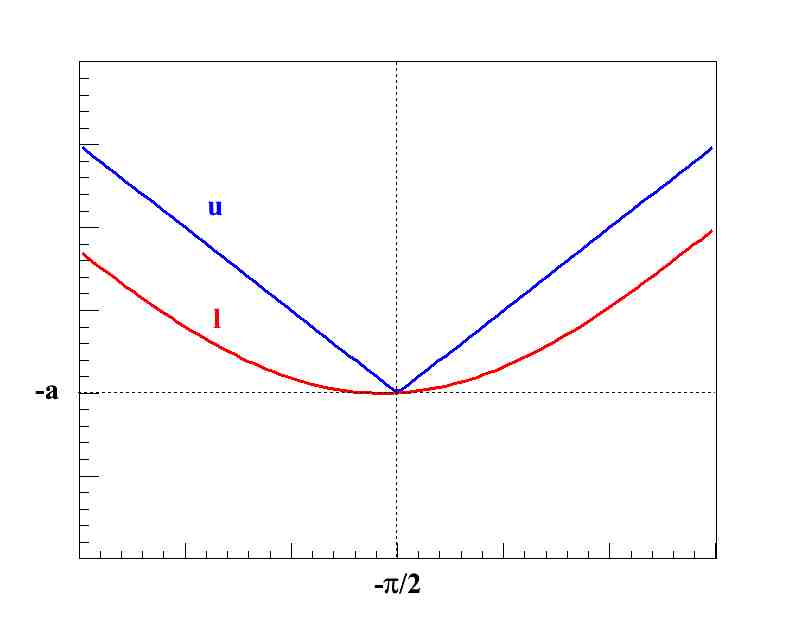
Plot the graphs of
and
on the same set of axes. Compute if f(x) is squeezed by l(x) and u(x) at
.
Step 1
Recall what it means for f to be squeezed by l and u and how we can apply the Squeeze Theorem to find limits.
Question 1
The function f is squeezed at x = c if there exist two functions l and u such that l(x) ≤ f(x) ≤ u(x) for all x ≠ c in an open interval containing c. Then if
we must have
.
This is called the Squeeze Theorem.
Step 2
Question Sequence
Question 2
Note that is always zero.
Based on the graphing techniques of shifting, stretching and reflecting, it has the shape of an absolute value graph y = |x| shifted π/2 units to the and 9 units .
Step 3
Use the Squeeze Theorem to find if f(x) is squeezed by l(x) and u(x) at x = π/2.
In order to use the Squeeze Theorem, we would need to show that . Then by the Squeeze Theorem,
would also be equal to L.
Question Sequence
Question 5
Either from the graph in Step 2, or the continuity of the functions, find and
.