Problem Statement

round(rand(11,25)/10.,1)
round(rand(12,28)/10.,1)
round(9*1.7/(4*3.14159265*1.7*1.7),3)

A conical tank has height 3 m and radius 2 m at the top. Water flows in at a rate of 1.7 m3/min. How fast is the water level rising when it is 1.7 m from the bottom of the tank?

 
Step 1

The water in the container forms a cone of radius R cm and height H cm. The given conical container has radius Rc = 2 m and height Hc = 3 m.

A vertical cross section looks like the figure shown.

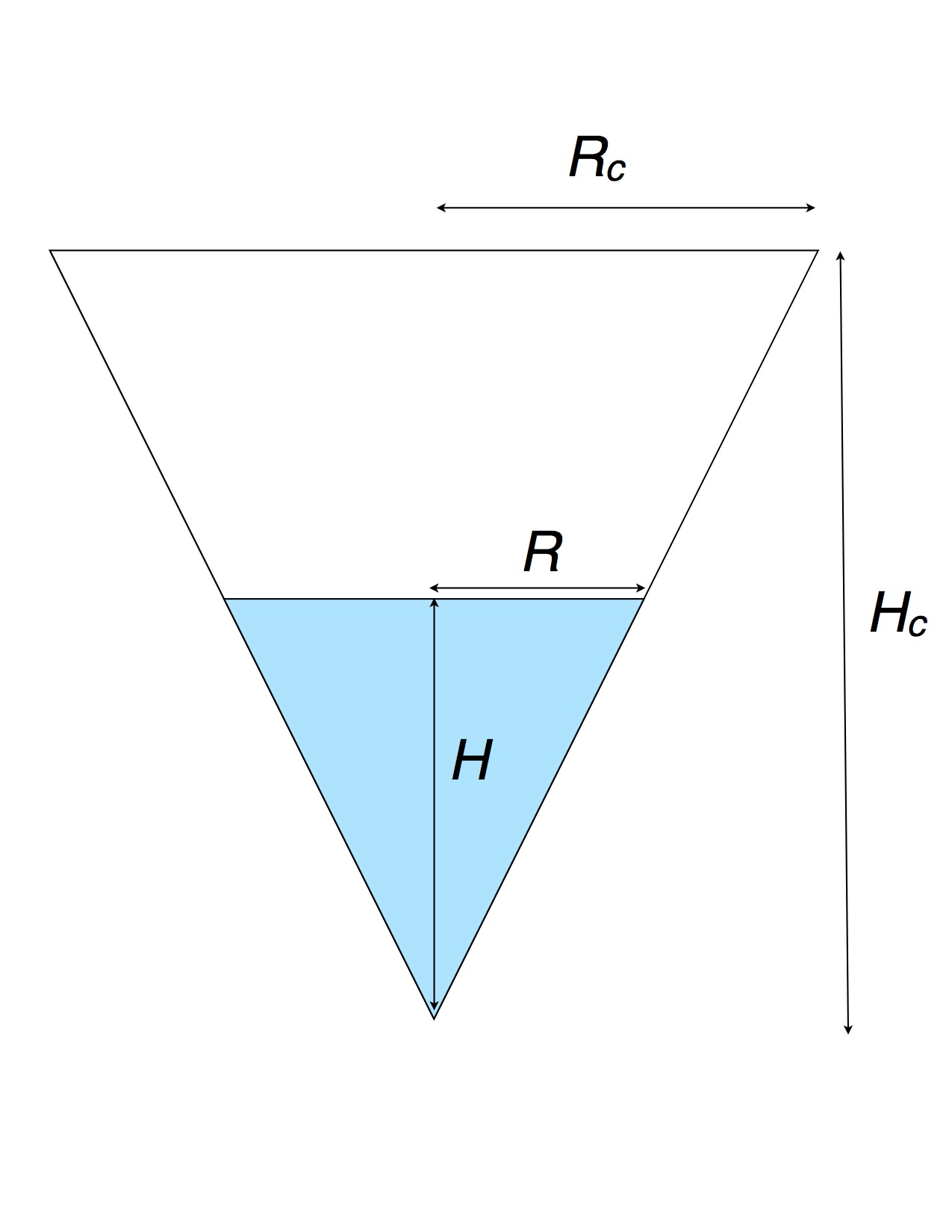
Question Sequence

Question 1

The "How fast?" question to be answered is "speed," the absolute value of velocity. The water level rises so the speed of the change in water level and the velocity are the same.

The velocity at which the water level changes is (where t is time in min).

Correct.
Incorrect.

 
Step 2

Because we don't have a value for R, we need to rewrite in terms of H only.

Use ratios of similar triangles, , (see figure below) to solve for R in terms of H for the given radius 2 m and the given height 3 m.

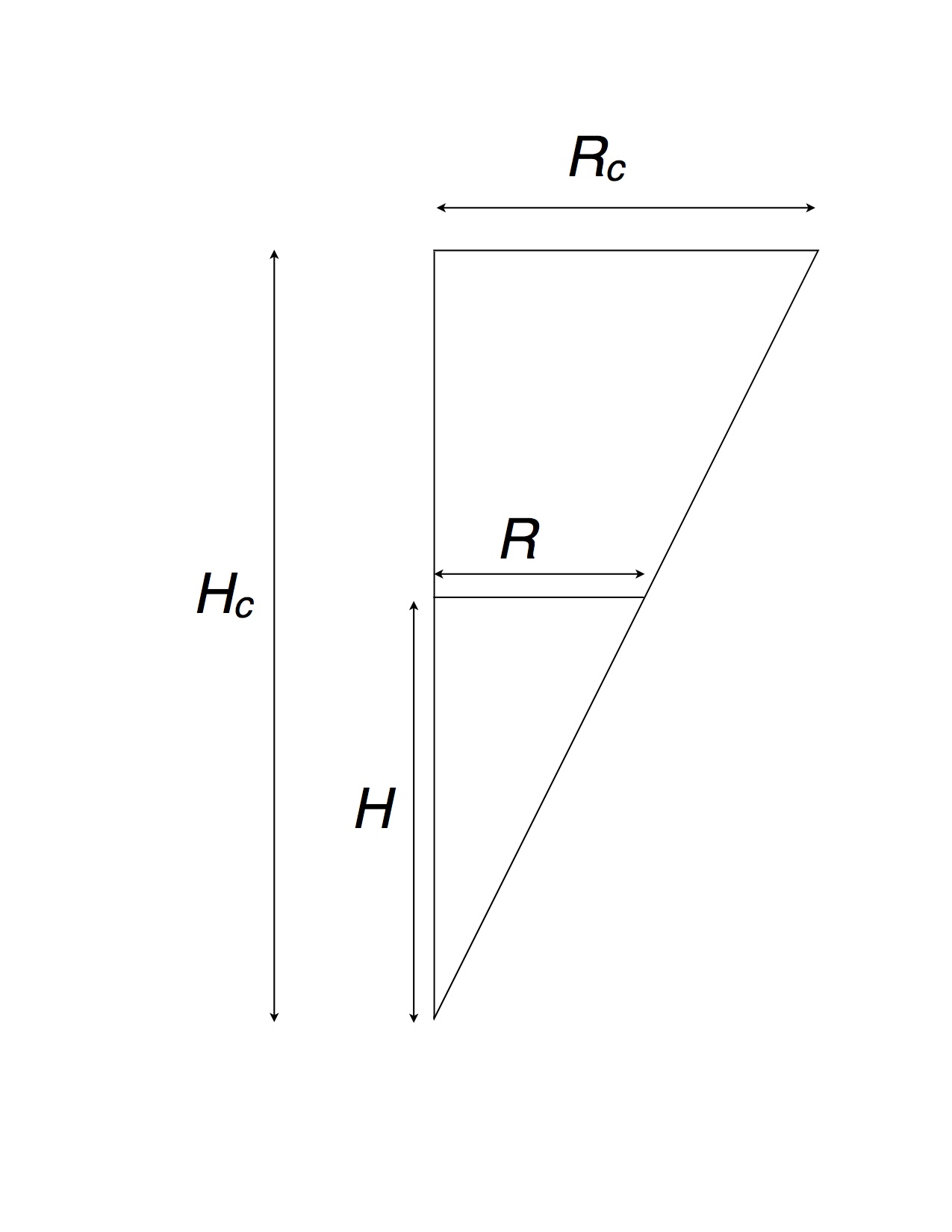
Question Sequence

Question 4

R = ·H

Correct.
Incorrect.

 
Step 3

Question 6

To get a related rates equation, implicitly differentiate with respect to t using the chain rule.

Keep in mind that V and H are functions of t.

[]

Correct.
Incorrect.

 
Step 4

Question 7

Substitute H = 1.7 m, dV/dt = 1.7 m3/min into the related rates equation, ; then solve for to find how fast the water level is rising in the conical tank at the instant the water level is at a height of 1.7 meters. (Round your answer to three decimal places.)

m/min

Correct.
Incorrect.