Let’s introduce inferential statistics in the context of an important empirical question: Does driving while talking on a cell phone affect one’s driving? Many legislators seem to think so: As of this writing, the use of handheld cellular telephones while driving has been banned in 14 states plus Washington, D.C., Puerto Rico, Guam, and the U.S. Virgin Islands. Many other states have left it to local jurisdictions to ban their use, including Massachusetts, Michigan, Ohio, and Pennsylvania. Note, however, that no state currently bans all drivers from using hands-free cell phones while driving. Presumably, the rationale behind this decision is that cell phones are harmful because they reduce the number of hands on the wheel from two to one. The loss of that hand is what causes individuals to drive carelessly; therefore, hands-free technology should restore the driver to conditions similar to those they experience when they’re simply talking to their passengers. Makes sense, right? Being a critical thinker, you are probably thinking, “Yes, but even the most commonsense beliefs should be regarded with skepticism. Show me the scientific evidence!” Likewise, if you’ve ever had the displeasure of driving behind people using even hands-free devices, you may have noticed that they still don’t seem as attentive as those who are simply talking to passengers.

A-15

Hunton and Rose (2005) investigated our opening question experimentally. They tested the hypothesis that driving performance would grow increasingly worse across three conditions: (1) during no conversation, (2) during a conversation with a passenger, and (3) during a hands-free cell phone conversation (for the purposes of this discussion, focus your attention on the last two conditions). Participants engaged in a realistic simulated driving task while they either spoke with a passenger seated to their right or with an individual on a cell phone using a hands-free device. Table A-5 includes data that could have been generated by this study.

The descriptive statistics indicate that the means between these two experimental conditions are different; those who used a hands-free device to talk committed more errors than those who simply spoke to a passenger. Note that we have new symbols for the number of people in each condition (n), for the mean (M), and for the standard deviation (s). These symbols indicate that we are working with samples rather than populations.

Based on the means, can you now conclude that hands-free devices cause declines in performance? Well, that depends on whether you can rule out two different classes of alternative explanations: one concerned with experimental design and one concerned with chance. Let’s first briefly review the explanation that has to do with experimental design, then move on to chance.

Recall from Chapter 2 that in order to comfortably make the claim that a manipulation caused changes in a dependent variable, you have to hold all other factors constant—factors having to do with preexisting differences between groups (e.g., personality traits, skills, motivation) and factors having to do with the research environment or procedure (e.g., the time of day the study is run, the setting in which it is held). Ideally, the only factor that should differ between conditions is the manipulation of the independent variable.

So, did this study (Hunton & Rose, 2005) pass this test? First, take a moment to think about what possible individual differences could have influenced participants’ performance during the driving simulations. If you reasoned that differences in individuals’ driving skills could be a factor, then you are on the same page as the researchers. How might they have controlled for these differences? People’s driving skills were controlled by—you guessed it—random assignment. Professional and amateur drivers had an equal chance of being assigned to either condition; thus, any differences in performance on the driving task couldn’t be attributed to preexisting differences between groups.

Of course, the researchers also had to be very careful to rule out alternative explanations having to do with the research procedure, so they held a number of environmental variables constant. For instance, participants in both conditions were told that the purpose of the study was to test the quality of the simulation software and that they would be observed by a representative of the manufacturer. The “representative,” who was actually a confederate of the researchers, was instructed to ask participants the same set of questions, in the same order, and at the same pace. This way, if the groups did differ, no one could argue that it was due to differences in the way they experienced the experimental procedure.

A-16

In summary, the researchers (Hunton & Rose, 2005) ruled out several alternative explanations for any differences they observed in the number of errors by randomly assigning participants to conditions and by treating both groups in exactly the same way, except for the manipulation. Are you justified in concluding that hands-free cell phone use leads to more crashes and less careful driving? In a word, no. You haven’t ruled out the possibility that our findings were simply due to chance. Inferential statistics will enable you to do this. As noted earlier, inferential statistics are mathematical techniques that enable researchers to draw conclusions about populations based on data collected from samples.

Imagine for the moment that someone wants to convince you he has a magic coin. You know that if the coin were not magic, and he were to flip it a bazillion times, there is a 50-50 chance that it would come up heads (or tails). Now you don’t have all the time in the world to sit there and watch this guy flip his coin, but imagine you’re willing to wait as he flips it 10 times. Further imagine that he comes up with 7 heads and 3 tails. Should you accept his claim that he is in possession of a magic coin? Probably not. Over trials lasting just a few coin flips, you know that there will be variations in the proportions of heads versus tails—variations that have more to do with chance and less with magic.

Here is your challenge, then: You want to test the hypothesis that this is a magic coin. You know that the most thorough and convincing test of this hypothesis would involve flipping the coin an infinite number of times, but by definition you cannot do that. Researchers face a similar problem when they want to test their hypotheses. For example, imagine a researcher wanted to test the hypothesis that the majority of the people in New Haven, Connecticut, prefer organically grown produce to conventionally grown produce. She knows that the most convincing test of this hypothesis would involve asking the entire population of New Havenites their preference, but she has neither the time nor the funding to do so. What would you recommend she do? If you carefully read Chapter 2, you recognize that this situation calls for representative sampling. You might recommend that she randomly select a sample of New Havenites, ask them “Do you prefer organically grown produce to conventionally grown produce?” then tabulate her results.

A-17

Imagine she finds that 56% of those sampled said they prefer organically grown produce. Can she reasonably conclude that her hypothesis is correct? Alert readers will point out that this depends entirely on how successful she was in selecting a representative sample. Even if the majority of people in New Haven prefer conventionally grown produce, she could, by chance alone, have randomly selected a sample that included a majority of people who prefer organic. How can she find out whether her results are attributable to chance? She might begin by asking, “If I repeatedly sampled the population of New Havenites, how often would I find results that disconfirmed my hypothesis?” As explained below, this is the question that essentially drives inferential statistics.

THE NULL VERSUS ALTERNATIVE HYPOTHESIS. The researcher above was interested in testing the hypothesis that most of the people of New Haven preferred organically grown produce. For the sake of introducing hypothesis testing, though, it may help to go back to the study that asked whether driving while talking with a hands-free cell phone is less safe than driving while talking with a passenger. Before you can answer this question, though, you’ll need to formally state some hypotheses about two populations: drivers who speak to passengers and those who talk on cell phones. Though it seems strange to think of these groups as discrete populations, we assume that the sample of people who participated in each of your study’s conditions was selected from them. Whenever scientists test hypotheses, they assume they are working with samples drawn from populations. In fact, inferential statistics is socalled because you use samples to make inferences about populations.

You will start by hypothesizing that in the populations from which you drew your samples, there are no differences in safety between those who talk to passengers and those who talk on cell phones. Why? Odd as it may sound, when researchers want to test a hypothesis, they begin by assuming it’s not true. In doing so, they test what is called the null hypothesis—which states that no relationship exists between the variables they are observing and that any relationship they do observe is attributable to chance. The null hypothesis for this particular study is that in the population of drivers who talk to passengers, people commit the same number of errors, on average, as in the population of drivers who talk on cell phones.

The hypothesis you are truly interested in, of course, is that there is a difference in the mean number of errors committed between the population of people who talk on a hands-free phone compared with the population of people who talk to a passenger. Researchers call this the alternative hypothesis (also known as the research hypothesis)—a hypothesis that states a relationship will exist between the observed variables. Let us now discuss how we will evaluate which of our hypotheses is more likely.

THE DISTRIBUTION OF SAMPLE MEANS AND SAMPLING ERROR. Earlier, you learned that when you sample from a population, you’re not always going to draw samples whose means perfectly represent the population’s mean. By chance alone, you could draw samples whose means differ from the mean of the population. The difference between the mean of the population and the means of the samples drawn from it is called sampling error.

To illustrate sampling error, imagine that you have a (very small) population consisting of four people whose scores are: 4, 6, 8, and 10, with a mean of 7. If you were to repeatedly draw samples of two people from this population, then replace them, how often would you obtain samples whose means were also 7? You can find out by listing all the possible combinations of samples of n = 2 people. Table A-6 lists all the possible samples of n = 2 you could draw from this population, as well as the means of those samples.

Each of those means is plotted on the frequency distribution graph depicted in Figure A-10. What do you notice about the shape of this distribution? It’s that standard normal distribution again! Most of your scores are clustering around a mean of 7— exactly what you’d expect, given that your samples come from a population with this mean. However, sometimes by chance alone you would draw samples whose means were not 7. Sometimes you might draw samples whose means are hardly representative of the population mean of 7—some as extreme as 4 and 10. When you randomly select people from this (or any) population, you won’t always get a sample whose mean perfectly represents the population mean. Again, these chance differences between the sample and population means constitute sampling error. Luckily, there is a far more efficient method by which you can determine how much sampling error exists. You simply calculate a statistic called the standard error. The standard error quantifies sampling error or chance and is used to help determine whether you can reject the null hypothesis. We will return to this point shortly.

A-18

What you just constructed by plotting the sample means for all possible combinations of samples is a distribution of sample means, which is a hypothetical distribution of all possible sample means of a given sample size from a specified population. Do researchers really plot the means for all possible combinations of samples? No, they don’t. As you’ve probably figured out by now, the distribution of sample means is hypothetical; no one would painstakingly list all possible combinations of samples of a given size just to find out the probabilities of randomly selecting various sample means. Statisticians have created computer simulations that calculate and plot these sample mean differences in frequency distribution graphs so that we don’t have to.

A-19

Psychologists use the distribution of sample means, also called a sampling distribution, to help them draw inferences about the probability of their particular data if the null hypothesis is true. In particular, they ask, “If the null hypothesis were true, how likely is it that we would observe the particular outcome of our study?”

Let’s return to the data presented in Table A-5, that is, the full group of 18 drivers in each condition studied. The mean number of errors committed by your sample of participants who spoke to a passenger was 7 and for your sample of participants who spoke to someone via hands-free cell phone, 9. Though your sample means differ by 2 errors, you have to entertain the possibility that you happen to have selected exceptional samples—that is, two samples whose difference does not represent the actual difference between the populations. We will now calculate a test statistic to tell us how unlikely it would be to observe this difference, if the null hypothesis is true.

SIGNIFICANCE TESTING AND t-TESTS. When you are interested in testing whether two groups’ means are different beyond chance, you will be evaluating differences between two samples in a statistical procedure called a t-test. The particular t-test you will learn about is often referred to as the independent-samples t-test.

You will use the data in Table A-5 to calculate something called the t-statistic, a statistic used in the t-test that is the ratio of the hypothesized difference against chance differences:

Take a look at the numerator of the t-statistic formula, in particular, the term “μ₁ − μ ₂,” which refers to the hypothesized difference between the experimental groups in the population. Because you’re testing the null hypothesis, you hypothesize this value to be 0; in other words, under the null you expect that there will be no difference between the two groups in the population from which you’re sampling. The term “(M ₁ − M ₂)” refers to the difference between our sample means. The denominator contains the standard error, which as mentioned previously is a value that quantifies sampling error or chance. The standard error for this example is .79, a value that takes into account the variability of your samples and sample size. Conceptually, it can be represented as

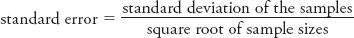
It was calculated following a procedure you can learn about when you take a class in statistics for the behavioral sciences. Plugging in the values to the t-statistic formula, you will find

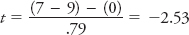
The fact that you have divided the mean difference by a standard score (the standard error) enables you to make use of the empirical rule to determine the probability of our data under the null hypothesis. Earlier, you learned that according to the empirical rule, about 68%, 95%, and 99% of scores tend to fall within 1, 2, and 3 standard deviations of the mean, respectively. The same rule applies even when the distribution is of sample means instead of scores and even when using the standard error instead of standard deviation. If 95% of scores tend to fall within 2 standard errors of the mean of the sampling distribution, then 5% of scores tend to fall outside of this region. These are values we would be less likely to observe if the null hypothesis were true. A t-statistic of ±2 would correspond to a mean difference that was highly improbable; the probability of observing it would be about 5%.

A-20

Our actual t-statistic, −2.53, was even more improbable; in fact, the actual probability of observing it happens to be about .02, which means that if the null hypothesis were true, you would have a 2% chance of obtaining a mean difference as extreme as this one. Consequently, you will happily reject the null hypothesis and conclude that driving while speaking on a hands-free cell phone results in more errors than driving while speaking to a passenger.

To reiterate, if the null hypothesis were true, the difference in errors you observed between your samples would have been so unlikely that you would be comfortable rejecting the null hypothesis. Researchers refer to this procedure as null hypothesis significance testing—the process through which statistics are used to calculate the probability that a research result could have occurred by chance alone. Your data were extremely unlikely under the null hypothesis, so you would conclude that your results were statistically significant, in other words, very unlikely to have occurred by chance alone.

How improbable should your observed difference have been for you to decide to reject the null hypothesis? This is up to the researcher; however, convention dictates that you set a probability level, or p-level, of .05, meaning the probability that you got these results by chance is 5%. The probability that our observed difference was due to chance, 2%, was lower than our 5% cutoff.

TYPE I ERRORS. Does having rejected the null hypothesis mean you can state with certainty that you proved the alternative hypothesis is true? In a word, no. When a researcher decides to set his or her p-level at .05, he or she is essentially saying, “My findings are unlikely to be due to chance. However, it is still possible that I selected samples whose mean differences were this extreme by chance alone and the probability of this is 5%.” In other words, whenever you reject the null hypothesis, you risk doing so incorrectly. You risk making what is called a type I error—rejecting the null hypothesis when it is, in fact, true. What is the probability of making a type I error? It is the probability level (the p-level) you set at the outset (more professionally referred to as the “alpha level”). Though your mean differences were unlikely to have been obtained by chance, the probability is not nil, so you can never feel comfortable saying that you proved the hypothesis to be correct (which is why researchers often prefer to say that they have “demonstrated” a relationship between variables).

VARIABILITY, SAMPLE SIZE, AND CHANCE. How does the amount of variability within a sample affect your ability to reject the null hypothesis? This can be answered in the context of the cell-phone experiment. You invited people into your lab and randomly assigned them to one of two groups. For the sake of this example, imagine that you manipulated your variable perfectly—you held all aspects of your experiment constant by randomly assigning people to groups and by treating everyone across each of the two groups in exactly the same way, except for your manipulation.

There’s still one aspect of the experiment over which you have no control: pre-existing individual differences. As we’ve discussed, people walked into your lab with their own unique learning histories, interests, moods, and importantly, driving skills. So even though you treated the groups in exactly the same way (except for the manipulation), and even though you randomly assigned them to conditions, you know at the outset that your manipulation isn’t going to make everyone within each of the groups get the same exact score. People differ. Figures A-11a and b depict pairs of hypothetical frequency distributions for groups whose means differ. The difference between Panel A and Panel B lies in how much variability exists within each of our passenger versus cell phone user groups. This will have implications for the conclusions that can be drawn about the effect of the manipulation and, by extension, about the null and alternative hypotheses.

A-21

Figure A-11a shows two frequency distributions: one for the passenger group and one for the hands-free cell phone group. Notice how little variability there is within each of these groups: The scores are tightly distributed around the means, such that the means represent the groups fairly well; the manipulation seems to have the effect of making everyone in each of the groups look basically the same. Note also that because little variability exists within the groups, there is very little overlap between these two distributions of scores; the people in the passenger group are so distinct from those in the hands-free cell phone group that you would feel fairly comfortable asserting that it was due to your manipulation and not chance.

Now take a look at Figure A-11b. These frequency distributions represent what would happen if the two samples still differed, on average, but had a lot more variability within them. Note how this increase in variability increases the amount of overlap between the two distributions of scores—it’s hard to even distinguish between them! If they do differ, on average, it’s difficult to make the case that it’s because of anything an experimenter did to them, since the effect of the manipulation was so inconsistent across people within each of the groups. Chance is probably playing a role here. If your samples’ data had been distributed like this, you would probably not be able to reject the null hypothesis.

Statisticians had exactly the above idea in mind when creating the formula for t. Here is the t-statistic formula again:

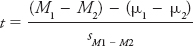
As noted, the term in the denominator, the standard error (s_{M1 − M2}), is calculated by dividing the standard deviation of the samples by the square root of n:

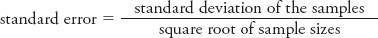
What’s important here is that the standard deviation is an index of how much variability exists within the samples. If there is a lot of variability, the standard deviation, and by extension the standard error, will increase. Keep this in mind as you take another look at the t-statistic formula. What would happen to the value of t if the standard deviation were to increase? As the standard deviation increases, t would decrease, as would your ability to confidently reject the null hypothesis.

A-22

So, how does sample size affect your ability to reject the null hypothesis? Read on for the intuitive answer and then the technical one. Whose data would you find more convincing for making the case that talking on hands-free cell phones is more dangerous than talking to a passenger while driving: Professor Small Sample’s, who found a difference between his samples, with only one person in each condition; or Professor Large Sample’s, who found the same difference, with 100 people in each group? If you remember the discussion of sample size, you should not have chosen Professor Small Sample’s data because you reasoned that two people hardly represent the population of drivers. For all you know, he could have by chance assigned auto racing driver Danica Patrick to the passenger condition and a visually impaired centenarian to the cell phone condition. But if Professor Large Sample detects the difference between samples using lots of people, you may start to think, “Maybe he’s onto something there….”

Again, the t-statistic formula takes this very idea into account in its calculation of the standard error. Take another look at the formula for the standard error; you’ll see that, as sample size increases, the standard error decreases. So if you’re planning a study and want to lower the probability that chance is playing a role in your results, recruit lots of people!

A-23

In your cell phone study, you ruled out chance as an explanation for the differences in errors between the cell phone and passenger groups. Should you now lobby your legislators to ban all cell phone use? Before you risk being ostracized by your community for taking away the joy of talking to loved ones while stuck in traffic, you need to consider whether the differences you observed were more than just statistically significant. You should consider whether the effect you observed was sizable. Effect size is a measure of how big the effect is; however, it’s more than that. It tells us how big the effect is when you control for the amount of variability that existed within your sample(s).

What the significance test told you was the probability that your differences are due to chance; it told you nothing about whether your findings were “significant” in the way you’re probably accustomed to using the term—that is, it didn’t tell you if your findings were important, newsworthy, or even noteworthy. Nor did it tell you how consistent the effect was across people. As an example, take a look at the fictional data depicted in Table A-7.

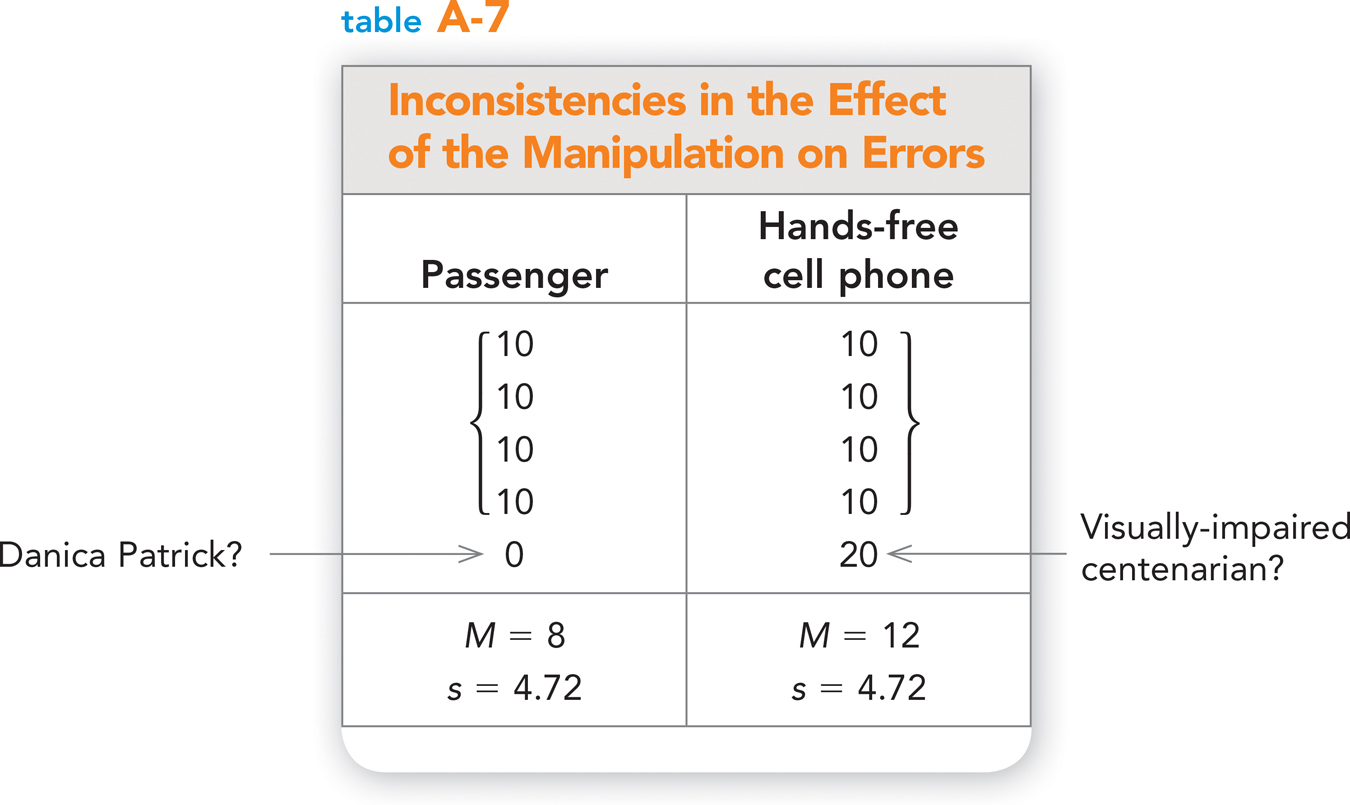
If you were to only pay attention to the mean differences between your groups, you might be quite impressed with the data: There is, on average, a difference of four errors between the two conditions. When you take a closer look, though, you can see that the effect of your manipulation wasn’t consistent from person to person—in fact, the effect was so inconsistent that the majority of participants were unfazed by it! Even if you had found, by doing a t-test, that your mean difference “beat chance” (it doesn’t—can you figure out why?), you’d have a hard time selling the idea that we should demand a ban on the use of cell phones while driving. The size of the effect is just too inconsistent from person to person—that is, there’s too much variability in the data.

“But you just told us that the standard error takes this variability into account!” you must be thinking. Yes, of course, you’re right: When calculating the standard error, you divide the variability within your groups (quantified by the standard deviation) by the square root of your sample size. Here’s where things get interesting. Because there is an inverse relationship between sample size and standard error, if an effect is inconsistent from person to person (as it is above), your findings can still be statistically significant. Check it out. Earlier, you found that there was a 2-point mean difference between your two groups. In calculating the t-statistic, you also learned that you were able to reject the null hypothesis, owing to the fact that your standard error was outweighed by the mean difference, by a factor of 2.53:

A-24

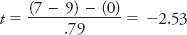
Recall that the standard error, your operational definition of chance, is calculated by dividing the standard deviation of our samples by the square root of your sample size.

Immediately you can see that even if there were a lot of variability within your cell phone and passenger conditions, a sufficiently large sample size could enable you to reject the null hypothesis; however, if there had been a lot variability in your data, it would’ve been hard to make the case that the effect of your manipulation had been fully consistent across people. In short, the size of your sample can work to reduce standard error enough so that you can reject the null, even if the effect doesn’t hold for most individuals.

So if sample size poses problems for the inferences we make about our data, what would you suggest we do? If you’re thinking, “Why not come up with a formula for effect size that takes into account the size of the effect and the consistency of the effect and that ignores sample size?” then you’re right on. Psychologists rely on a number of formulas for determining effect size. The formula to focus on here is Cohen’s d:

Cohen’s d is a measure of effect size that expresses the difference between sample means in standard deviation units. Cohen’s d offers a benchmark against which you can evaluate the size of your differences. These criteria, set forth by Cohen (1992), are presented in Table A-8.

In the cell-phone study, the absolute mean difference between our groups was 2 and the standard deviation, which was calculated for you, was 3.35, and so d would be

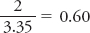
In this example, your d indicates you have a medium effect, because .60 is closest to the cutoff of .50. What you have just learned is that participants in your cell-phone group committed, on average, 0.60 of a standard deviation more errors than your passenger drivers.

Is it time to call the legislators? Well, notice first that the above table provides standardized guidelines, but not standardized recommendations (e.g., “Medium effect: Start panicking”). The decision concerning how to act, armed with your data, will depend on various considerations. For instance, your dependent variable happened to be errors, but what if the numbers referred not to errors but to highway fatalities? In this circumstance, you might wish to call your legislators right away (but not while driving). Statistics do not do our thinking for us—they are instead tools that enable us to make informed decisions on our own. Finally, remember that these data, while based in reality, are not the actual data from the study. You are encouraged to read the actual study!

A-25