Game Theory

Technology standards are constantly changing. Compare your current smartphone with your previous one and notice the features that have become standard, such as voice recognition typing and advanced GPS applications. Behind the scenes, technology firms such as Apple and Samsung engage in fierce competition in the development of the next technological feature. But developing a new feature itself is not enough; to become the industry standard, all firms must adopt compatible features. Meanwhile, competing firms strive to improve upon existing features to avoid becoming obsolete and losing market power. The study of how oligopoly firms use strategies to gain market power and their effects on competing firms and on consumers form the foundation of game theory.

What do Warren Buffett, Bill Gates, Annie Duke, and Mike McCarthy have in common? They are all experts in strategic thinking.

Reuters/CORBIS
Jacob Andrzejczak/Getty Images
Dan Kelly Photo/Corbis

Game theory is the study of how individuals and firms make strategic decisions to achieve their goals when other parties or factors can influence that outcome. In short, it is the study of strategy and strategic behavior and is used in any situation in which one must predict the actions of others and respond by choosing among more than one strategy, each resulting in a potentially different outcome. Although game theory was first developed from the analysis of imperfect competition, particularly in explaining the actions of firms that are oligopolies, today it is used to study situations that extend well beyond the typical economic problems we have seen thus far in this book.

Real-life applications of game theory are abundant, and include situations common in sports coaching, business pricing, management, politics and elections, law and courtroom proceedings, military strategy, and even literal games such as poker. In 1995, Johnnie Cochran successfully defended O. J. Simpson against a murder charge when the evidence seemed to be stacked against him. In 2004, Annie Duke became the world’s top female poker player by winning the World Series of Poker Tournament of Champions. In 2005, Bill Belichick took his New England Patriots to an unprecedented third Super Bowl win in four years. In 2008, Barack Obama surpassed favored Hillary Clinton to become his party’s presidential nominee and eventually the president. As these events suggest, the importance of strategic thinking is a reason why game theory is an interdisciplinary topic that extends well beyond economics.

This section highlights key concepts of game theory, beginning with the important concept of a Nash equilibrium, named after famous mathematician-turned-economist and eventual Nobel Prize winner John Nash. In the next section, we extend this analysis to realistic cases and applications to illustrate how game theory is a part of our lives. We will show how game theory helps explain the actions of oligopolies.

NOBEL PRIZE JOHN NASH

No person arguably has had more influence on strategic economic analysis than John Nash, a mathematician turned economist whose theories led to the development of modern game theory. Born in 1928 to well-educated parents in Bluefield, West Virginia, John Nash was encouraged to pursue educational interests at a young age. As his aptitude for math developed, he enrolled in advanced mathematics classes at a local college while still in high school.

At age 16, he attended the Carnegie Institute of Technology (now Carnegie Mellon University), where by age 20 he earned both his bachelor’s and master’s degrees in mathematics. His advisor wrote a one-line letter of recommendation for his graduate school applications: “This man is a genius.” Nash continued his education at Princeton University where he earned his Ph.D. at age 22, completing what remains one of the shortest yet most influential dissertations: a 28-page study of noncooperative games whose conclusion would eventually be coined the Nash equilibrium.

John Nash worked as a professor at the Massachusetts Institute of Technology and also for the U.S. government as an expert code breaker. It was during these early adult years when mental illness began to set in, and he eventually was diagnosed with paranoid schizophrenia. His battles with severe disillusions consumed much of his life, and he was often seen talking to imaginary figures. Yet, his ability to make new contributions to game theory, a relatively new topic at the time, earned him a permanent faculty position at Princeton, where he remains a professor to this day.

In 1994, John Nash was recognized with the Nobel Prize in economics for his contributions to game theory. His life would be the subject of several books, including Sylvia Nasar’s A Beautiful Mind, published in 1998. The book was adapted into the 2001 blockbuster movie by the same name, starring Russell Crowe, that would go on to win four Academy Awards, including Best Picture.

Basic Game Setup and Assumptions

A basic setup of a “game” requires players, information, strategies, outcomes, and payoffs. This game setup applies to virtually all situations in which strategy (game theory) is used to analyze a real-life scenario. Let’s look at each component.

• Players: Players can be firms competing for customers, a plaintiff and a defendant in a courtroom, two or more countries at war, or actual players in the literal sense in a sporting match or card game.
• Information: Each player holds information that is either known to others or is private. Having private information changes the way in which a game is played and the outcomes it produces.
• Strategies: Players make choices based on strategies devised from the information they have and the information they suspect other players hold. Players use strategies to improve the likelihood of achieving their best outcome.
• Outcomes: Outcomes refer to all possibilities, good and bad, that can occur given the strategies employed by players. In zero-sum games, outcomes are a “win” or a “loss.” In any given hand in poker, for example, one person wins the pot of money while everyone else loses. In other games, there may be no losers per se, but firms compete for market share, or job applicants compete for various types of jobs.
• Payoffs: The payoff is the value players attach to each outcome. Each player has his or her own perception of each outcome, because rarely do players in a game have exactly the same objective. Payoffs are what players ultimately try to maximize.

In addition to identifying the setup described above, analyses of situations involving game theory typically make two general assumptions:

1. Preferences are clearly defined. The objectives of each player must be known. For example, a firm’s objective might be to maximize its profits, while a golfer’s objective is to achieve a low score.
2. Players rationally choose strategies to achieve objectives. Players make consistent decisions that improve their chances of achieving their goals. Sometimes, however, people make decisions that seem irrational. Game theory does have something to say about irrational behavior, but this is beyond the scope of this section.

Simultaneous Versus Sequential-Move Games

Game theory moves can be simultaneous or sequential. Simultaneous-move games involve actions by players that occur at the same time. Examples include sporting matches such as a soccer game with offensive and defensive players, and business pricing where firms must decide on prices to be placed in ads without knowing what prices their competitors will choose. Sequential-move games are situations in which one player at a time makes a move. Examples include games such as chess or tic-tac-toe, but also extend to examples such as negotiations (where offers are made back-and-forth), golf, or reality show competitions.

The way in which simultaneous-move and sequential-move games are analyzed differs. We focus primarily on simultaneous-move games, leaving the discussion of sequential-move games to later in the chapter.

Simultaneous-Move Games

Figure 6 illustrates a two-player simultaneous-move game in a diagram called a game table (also known as a payoff matrix or normal form analysis). In our example, Lowe’s and Home Depot must choose one of two policies: advertise in the local paper or don’t advertise. Lowe’s strategies are listed in rows, while Home Depot’s strategies are listed in columns. Because players (firms) move at the same time, outcomes are determined by the interaction of strategies chosen by each player. In this case, four potential outcomes exist, with Lowe’s payoff shown before Home Depot’s in each outcome. The outcome depends on which strategy each player actually chooses.

Simultaneous-Move Game Illustrated in a Game Table A simultaneous-move game between Lowe’s and Home Depot is shown in which both firms must choose whether to advertise in the local paper or not, without knowing what the other will do. The choice made by each firm results in a different payoff for each.

Let’s go through each outcome, to show you how to read the figure. If Lowe’s and Home Depot both advertise, each will earn a profit of $100,000. The advertising will induce some customers to buy now, but won’t much affect whether they will buy at Lowe’s or at Home Depot. There is a cost to advertising, which is why profits are lower when both firms advertise than when both do not. When both do not advertise, each earns a profit of $200,000. Customers continue to go to Lowe’s and Home Depot about equally, and both firms do not bear the cost of the advertising.

What happens if one advertises while the other does not? The one that advertises increases profits. If Lowe’s advertises while Home Depot does not, it earns a profit of $300,000 compared to Home Depot’s $50,000. Why this result? Lowe’s has to pay the cost of advertising but more than makes up for it by taking customers away from Home Depot. By not advertising, Home Depot saves on this cost, but it does not make up for the lost customer sales. This result is the same, but reversed, if Lowe’s does not advertise while Home Depot does: Home Depot sees $300,000 in profits while Lowe’s profit is only $50,000.

Strategically, what is the best thing for each to do: advertise or not advertise? Let’s first look at the best possible outcome for Lowe’s. Its best outcome would be to advertise when Home Depot does not, allowing Lowe’s to earn $300,000 while Home Depot ends up with $50,000, its worst outcome. Alternatively, the best collective outcome for Lowe’s and Home Depot occurs when both do not advertise and each earns $200,000. Is either of these outcomes likely?

Let’s approach this question by looking at the best response of one firm to the other’s action. Suppose Home Depot strives for its highest possible outcome of $300,000 by advertising. What would be Lowe’s best response? Clearly, Lowe’s does not want to bear the minuscule profits of $50,000 if it does not advertise and Home Depot does advertise, therefore it advertises and earns $100,000. Therefore, choosing to advertise is a best response if competitors advertise. In Figure 6, this payoff is underlined.

Looking at it from Home Depot’s point of view, it also advertises in response to Lowe’s advertising, because it too would not want Lowe’s to grab too many of its customers. Advertising is a best response for Home Depot because it results in a payoff of $100,000 (underlined) instead of $50,000. If both Lowe’s and Home Depot act strategically by advertising to avoid the worst possible outcome, then the best case scenario of earning $300,000 is not possible.

If the best outcome is not possible, then how about the best collective outcome in which both firms choose not to advertise and each earns $200,000? Clearly, this outcome is better than if both firms advertise. But they cannot call each other up and say “I will not advertise if you do not advertise.” This is collusion, prevented by law in the United States and in many other countries. Each firm has to make a decision without knowing what the other will do.

Again using the best-response approach, if Home Depot chooses not to advertise, Lowe’s would still be better off advertising, because (1) it eliminates the worst-case outcome if Home Depot does in fact advertise, and (2) if Home Depot does not advertise, advertising would allow Lowe’s to achieve its highest payoff of $300,000. Therefore, Lowe’s best response to Home Depot not advertising is still to advertise (the corresponding payoff is underlined in Figure 6). From Home Depot’s perspective, its best response if Lowe’s does not advertise would be to advertise as well.

In sum, the best action each firm can take, considering each of the possible actions the other might take, is to bear the cost of advertising. This outcome is what economists call a Nash equilibrium.

Nash Equilibrium

A Nash equilibrium occurs when all players in a game use an optimal strategy in response to all other players’ strategies. It is the outcome that maximizes all players’ expected payoffs (the value of each potential outcome times the probability of that outcome occurring) given the information they have. In other words, aiming for the outcome with the highest payoff is not always prudent if the likelihood of achieving that outcome is small. Solving for Nash equilibrium is therefore valuable because it represents a player’s best payoff taking into account the self-interested actions of all other players affecting the outcome. Once a Nash equilibrium is achieved, no individual player can do better by changing his or her mind.

For example, it is possible that Lowe’s or Home Depot could see higher profits if it chose not to advertise, but there’s a higher probability of it leading to lower profits. Nash equilibrium guides players to choose strategies that result in the best expected payoff. In the Lowe’s–Home Depot example, the Nash equilibrium is for each to advertise when neither knows what the other will do.

An outcome is a Nash equilibrium if it results from all players acting strategically (using a best response) to each other’s actions. In some cases, players choose the same action regardless of what others do, while in other cases, players choose different actions in response to other players’ actions. In the Home Depot–Lowe’s example, each firm’s best response is to advertise regardless of what the other firm does, and is known as a dominant strategy. A dominant strategy occurs when one player chooses the same action regardless of what the other player chooses. When both players have a dominant strategy, a single Nash equilibrium will result. For Lowe’s and Home Depot, both advertising is the Nash equilibrium. But not all Nash equilibria are the result of dominant strategies. In fact, games need not be limited to one Nash equilibrium. When dominant strategies do not exist, games can have no Nash equilibrium while others might have more than one, as we’ll soon see.

Also, a Nash equilibrium outcome is not always obvious. In Figure 6, it might seem that Lowe’s and Home Depot not advertising would be a Nash equilibrium; besides, the profits for both are higher than the profits with advertising. But such a quick conclusion does not take into account the fact that one firm could do even better by advertising if the other does not. And because neither firm wishes to risk the worst-case scenario, they both engage in advertising as their best response action. Fortunately, not all Nash equilibrium outcomes are so pessimistic. In many cases, acting in response to another player’s actions can lead to a good outcome for all players, as we’ll see next.

Nash Equilibrium: A Personal Example Let’s look at a personal example to make sure that the idea of a Nash equilibrium is clear. Suppose you are talking with a friend on the phone, and the line suddenly goes dead. Does this scenario sound familiar? Perhaps it is because it happens so often. This very moment often creates a quick but annoying dilemma: Do you immediately call your friend back, or do you wait for your friend to call you back?

For simplicity, assume you are given just one opportunity to make a decision. If both you and your friend immediately call each other back, chances are you might end up reaching each other’s voicemail. If instead, you both wait for each other to call back, then you end up waiting anxiously wondering why your friend didn’t call you back. In each situation, players did not accurately select the best response to the other player’s action. Therefore, a Nash equilibrium occurs when one person calls and the other responds by waiting.

Figure 7 illustrates each of the four possible outcomes. Two outcomes meet the criteria for a Nash equilibrium, which is common for coordination-type games when players are attempting to achieve a mutually beneficial outcome. For each Nash equilibrium, both you and you friend used a best-response action that led to a completed call; in other words, if your friend calls, you wait. If your friend waits, you call.

Dropped Call Dilemma: Who Should Call Back First? The two cases in which the call is successfully connected each represent a Nash equilibrium.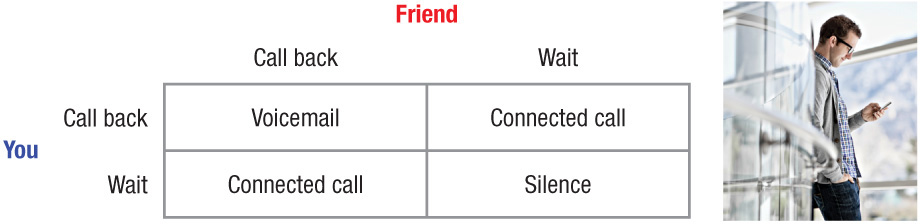

Tim Pannell/Corbis

To review, a Nash equilibrium describes any outcome when all players respond optimally to all possible actions by other players. At that outcome, no player would choose to deviate unilaterally from that outcome; this doesn’t mean that a better outcome might prevail with some cooperation, but rather that no player would change her position by herself. Finding a Nash equilibrium is therefore useful because it represents the best outcome given the self-interested actions of all other players.

We have seen two situations with different Nash equilibrium outcomes. For Lowe’s and Home Depot, the Nash equilibrium was an outcome that neither firm truly desired. In the next section, we will classify these outcomes as a Prisoner’s Dilemma and show what can be done to overcome such outcomes. For the dropped call example, we found more than one Nash equilibrium in which both players would be happy. But we need not stop here. The next section will highlight other Nash equilibrium outcomes that can result depending on the circumstances facing each player. Because the Nash equilibrium in each situation is not automatically obvious, it’s important to use the best-response method to solve for Nash equilibrium to ensure that each player’s expected payoff is maximized.