Production in the Short Run

Production is the process of turning inputs into outputs. Most products can be made using a variety of different technologies. As discussed earlier, these can be either capital-intensive or labor-intensive. The type of technology a firm chooses will depend on many things, including ease of implementation and the relative cost of each input into the process.

Again, in the simplified model we are working with, firms can vary their output in the short run only by altering the amount of labor they employ, because plant capacity is fixed in the short run. The extent to which output will change from adding labor depends on the ability to specialize in tasks and use other resources efficiently. But like all resources, labor is eventually subject to diminishing returns. Therefore, an individual firm’s production possibilities will follow the same general pattern as the production function for the entire economy introduced in Chapter 2. In the short run, output for an existing plant will vary by the amount of labor employed. This output is referred to as total product.

Total Product

Let’s examine some production basics by assuming that you start your own firm. Imagine that you decide to begin manufacturing windsurfing sails in an old warehouse that you rent. Your physical plant is constrained in the short run by the size of the manufacturing facility. Table 2 lists your firm’s total output (total product) as you hire more workers.

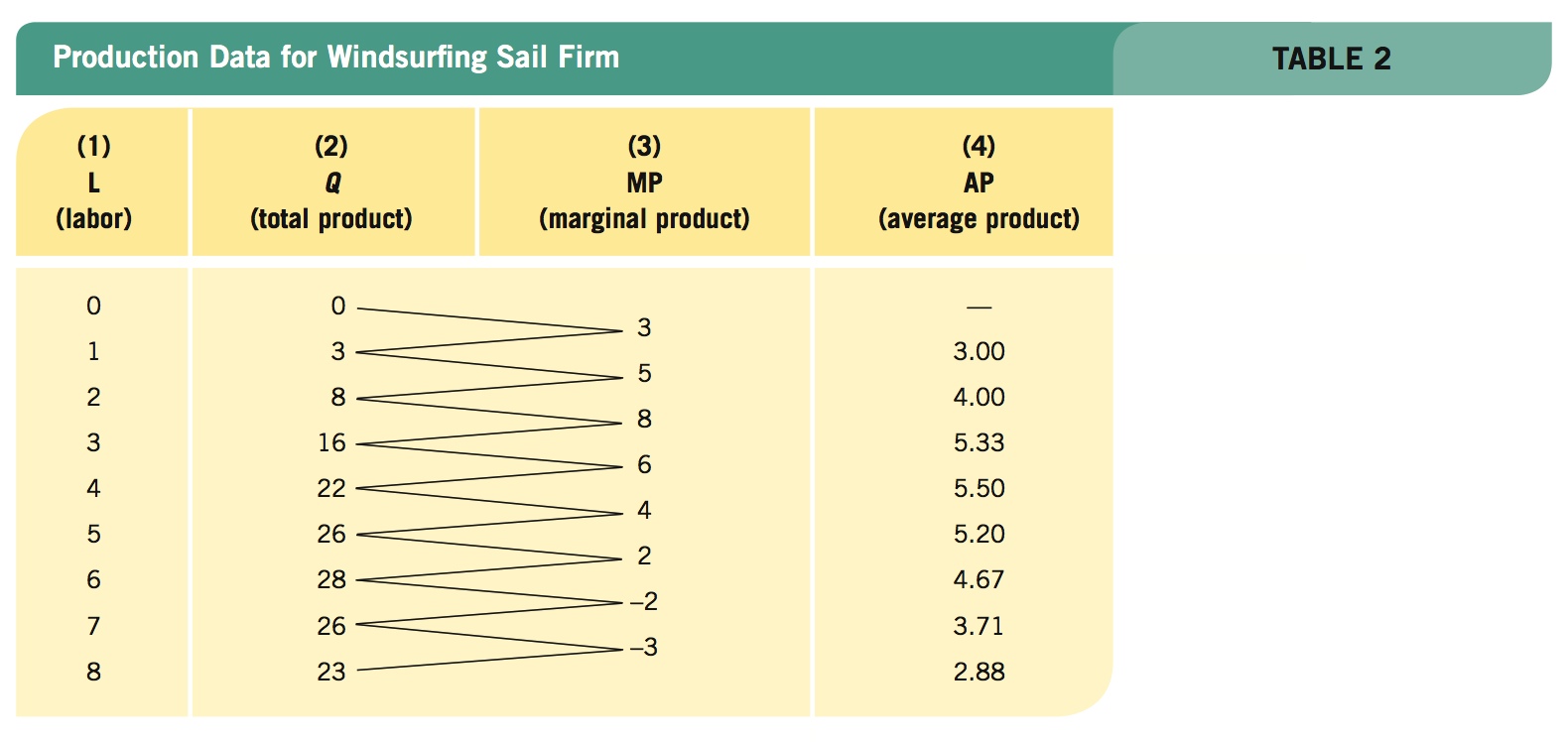
Panel A of Figure 1 displays your total product curve for windsurfing equipment, based on the data in columns (1) and (2) of Table 2. Output of sails varies with the number of people you employ. Output rises from 0 to 16 when 3 people are working to a maximum of 28 when 6 people are employed (point b). As you continue to hire employees beyond 6, you encounter negative returns. Total output actually begins to fall, possibly because the workplace has become overly crowded, confusing, hazardous, or noisy. Clearly, hiring any more than 6 employees would be counterproductive, because output falls but costs (such as the total wages of all the employees) rise.

Total Product Curve, Marginal Product, and Average Product These two panels show the relationship between additional labor and productivity. Panel A shows how increasing labor increases productivity, up to a point. Panel B shows marginal and average product. Marginal product reaches its maximum as the third worker is hired, after which marginal product starts decreasing. Total product keeps increasing, however, until you hit 6 employees. At that point, marginal product becomes negative, meaning that each additional employee actually reduces production.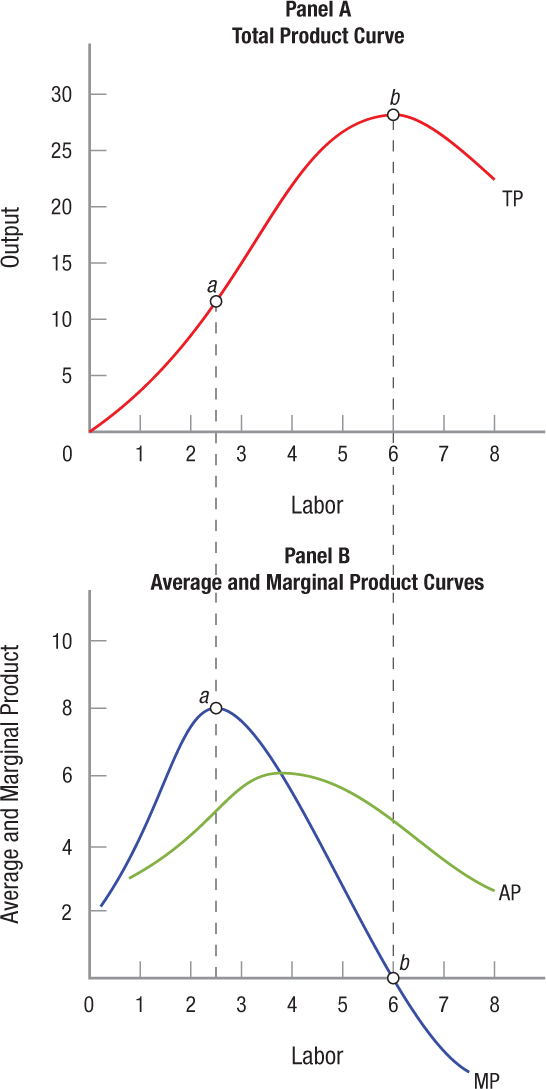

Marginal and Average Product

Marginal product [column (3) in Table 2] is the change in output that results from a change in labor input. Marginal product is computed by dividing the change in output (ΔQ) by the change in labor (ΔL). The delta (Δ) symbol is used to denote “change in.” Thus, marginal product (MP) is equal to ΔQ/ΔL; it is the change in output that results from adding additional workers.

Notice that when employment rises from 2 workers to 3 workers, output grows from 8 to 16 sails. Marginal product is therefore 8 sails at this point (point a in panel B of Figure 1). This is shown graphically with a point placed between the second and third worker, because this represents the change in output going from 2 workers to 3 workers. Contrast this with a change in employment when 6 people are already employed. Adding another employee actually reduces the total output of windsurfing sails from 28 to 26, therefore marginal product is −2 from the sixth to the seventh worker.

Average product (AP) or output per worker is found by dividing total output by the number of workers employed to produce that output (Q/L). Average product is shown in panel B of Figure 1. When employment is 3 people and output is 16, for instance, average product is 5.33.

Increasing and Diminishing Returns

In our example, each of the first three workers adds more to output than the previous worker hired. Therefore, the marginal product going from zero to one worker, one to two workers, and two to three workers increases. This is called the increasing marginal returns portion of the curve. In this range, output grows faster as you employ additional labor.

However, after you have employed three people, marginal productivity begins to trail off. Between three and six workers, you face diminishing marginal returns because each additional worker adds to total output, but at a diminishing rate.

Finally, once you have hired six employees, if you hire any more, this will result in negative marginal returns. Therefore, the marginal product curve crosses the horizontal axis at the sixth worker, which corresponds to the highest point on the total product curve (point b in Figure 1). Hiring additional people will actually reduce output, therefore rational firms never operate in this range.

Meanwhile, the average product curve follows a similar path as the marginal product curve, although there isn’t as dramatic a change as each worker is added. Average product gives you a sense of the overall productivity of a firm. The relationship between marginal product and average product is an important one. When marginal product exceeds average product—when a new worker adds more to output than the average of the previous workers—hiring an additional worker increases average productivity. This might be because hiring more people allows you to establish more of a production line, thereby increasing specialization and raising productivity. The marginal product curve always crosses the average product curve at its highest point, because once marginal product falls below the average product, the average product must fall as well.

Firms hire workers to produce output based on available resources, many of which are fixed in the short run. By adding more workers, firms can increase productivity by allowing workers to specialize in tasks for which they are more suited. As more workers are hired, diminishing or even negative returns can set in. The typical production curves shown in Figure 1 embody the law of diminishing returns. All firms eventually face diminishing marginal returns, but this does not mean production should be avoided as long as the value of the additional output produced exceeds the additional costs.

This analysis is important because it shows how much output is generated based on the number of workers hired, which will eventually translate into revenues for the firm once the output is sold. Therefore, production is an important component of profits, but not enough to determine the optimal production output. To maximize profits, we must also evaluate the costs of production, to which we turn next.