Costs of Production
Production tells only part of the story. We have to calculate how much it costs to produce this output in order to figure out if it is profitable to do so. Let’s now bring resource prices, including labor costs, into our analysis to develop the typical cost curves for the firm, both in the short run and the long run.
Short-Run Costs
In a very straightforward way, production costs are determined by the productivity of workers. Ignoring all costs except wages, if you, by yourself, were to produce ten pizzas an hour and you were paid $8 an hour, then each pizza would cost an average of 80 cents to produce—the cost of your labor. Yet, to ignore any other costs would be to neglect a significant portion of business expenses known as overhead.
To begin developing the concept of overhead specifically, and production costs more generally, remember that production periods are split into the short run and the long run. In the short run, at least one factor is fixed, whereas in the long run, all factors are variable. This has led economists to define costs as fixed and variable.
fixed costs Costs that do not change as a firm’s output expands or contracts, often called overhead. These include items such as lease payments, administrative expenses, property taxes, and insurance premiums.
variable costs Costs that vary with output fluctuations, including expenses such as labor and material costs.
Fixed and Variable Costs Fixed costs, or overhead, are those costs that do not change as a firm’s output expands or contracts. Lease or rental payments, administrative overhead, and insurance premiums are examples of fixed costs—they do not rise or fall as a firm alters production to meet market demands. Variable costs, on the other hand, do fluctuate as output changes. Labor and material costs are examples of variable costs, because making more products requires hiring more workers and purchasing more raw materials.
Certain costs don’t always fall so neatly into these two categories. For example, a new wireless communications tower can serve thousands of customers at the same cost as serving one (and resembles a fixed cost), but once capacity is reached, a new tower is needed (and resembles a variable cost). These types of costs are known as incremental costs. To keep things simple, however, we will assume that all costs fit into either the fixed or variable cost categories, such that total cost (TC) is equal to total fixed cost (FC) plus total variable cost (VC), or
TC = FC + VC

Blaine Harrington/age fotostock
Marginal Cost Although measuring total cost is important in determining the overall profitability of a business, the decision of whether to increase or decrease production largely depends on how total costs change when one increases or decreases the quantity produced. If the additional cost of producing one more unit of a good is greater than the additional revenue earned from that unit, then this unit would not be worth producing. Therefore, it is important to measure the change in costs with each additional unit of output produced.
Let’s return to the windsurfing sail business example. Suppose your firm has orders for ten windsurfing sails this month, and you get an order for one more sail at the last minute. Just how much would this additional windsurfing sail cost to produce? Or, in the language of economics, what is the marginal cost of the next sail produced?
marginal cost The change in total costs arising from the production of additional units of output (ΔTC/ΔQ). Because fixed costs do not change with output, marginal costs are the change in variable costs associated with additional production (ΔVC/ΔQ).
Marginal cost is the change in total cost arising from the production of additional units of output. Marginal cost (MC) is equal to the change in total cost (ΔTC) divided by the change in output (ΔQ), or
MC = ΔTC/ΔQ = ΔFC/ΔQ + ΔVC/ΔQ
Note that, for simplicity, we have been discussing changes of one unit of output, but we can calculate MC for a change in output of any amount by plugging in the appropriate value for ΔQ. And because fixed costs do not vary with changes in output, ΔFC/ΔQ = 0, and thus marginal cost is also equal to just ΔVC/ΔQ.
Table 3 provides us with more complete cost data for your windsurfing sail business. Assuming that you pay $1,000 per month in rent for the warehouse, fixed costs equal $1,000 [column (2)]. Your variable costs (the wages you pay your employees plus the price of raw materials) vary depending on the number of sails produced, and is shown in column (3). The total cost, therefore, is the sum of fixed and variable cost and is shown in column (4). Marginal cost measures the change in total (or variable) cost with each additional sail produced, and is given in column (5).
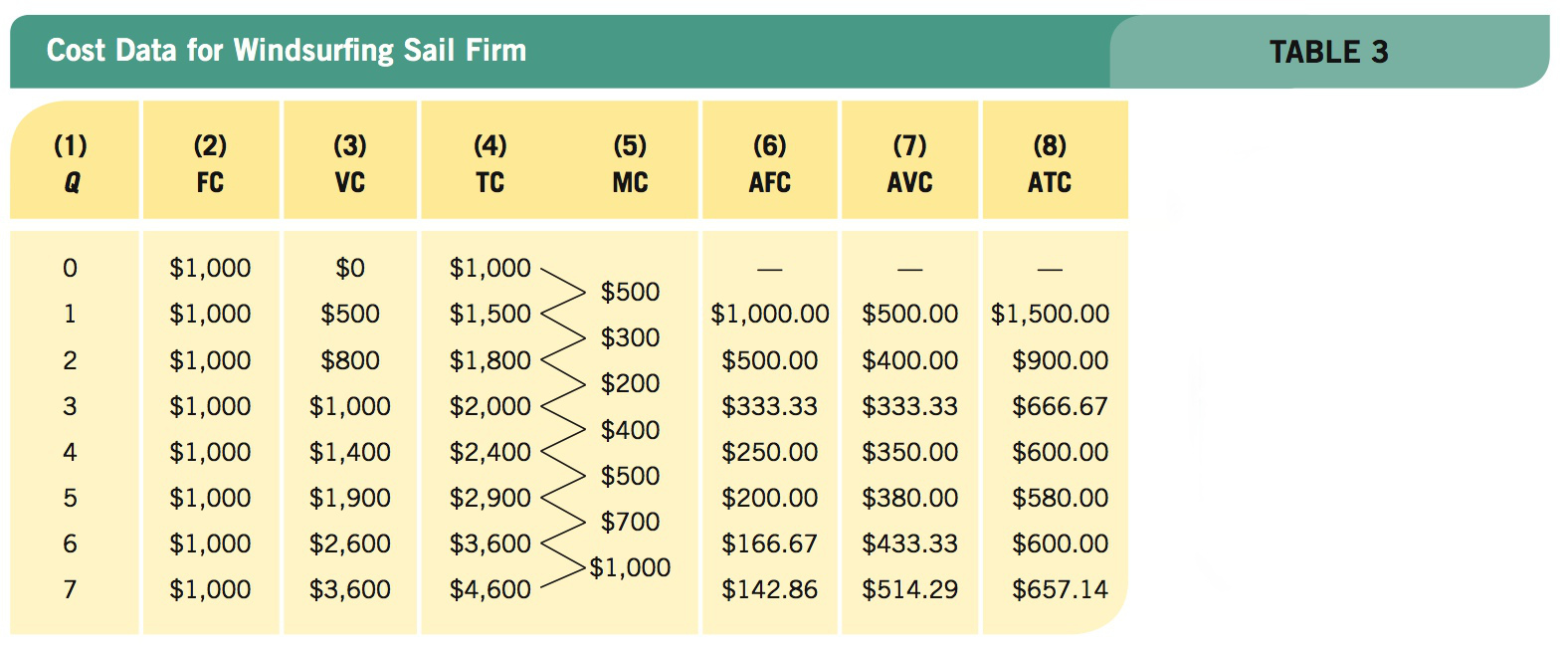
Let’s go through one row so that you can be sure of how we arrived at the numbers in columns (2) to (5). Looking at the row showing 4 sails, the fixed cost is $1,000 because this does not change based on the number of sails produced. Variable cost does change, because more work hours are needed to produce more sails; to produce 4 sails, the variable cost is $1,400. Total cost is simply fixed cost plus variable cost, or $2,400 for 4 sails. Finally, the marginal cost of the fourth sail is the change in total cost from producing 3 sails ($2,000) to producing 4 sails ($2,400). Therefore, the marginal cost of the fourth sail is the change from $2,000 to $2,400, or $400, and is shown in column (5) between the third and fourth units. It is common for marginal costs to first fall and then rise, which gives the marginal cost curve the distinct shape, which we will see later.

Average Costs When a firm produces a product or service, it typically wants a breakdown of how much labor, raw material, plant overhead, and sales costs are imbedded in each unit of the product. Modern accounting systems permit a detailed breakdown of costs for each unit of production. For our purposes, however, that level of detail is not necessary. For us, cost per unit of output (or average cost), average fixed cost, and average variable cost are sufficient.
If we divide the total cost equation (TC) by total output Q, we get
TC/Q = FC/Q + VC/Q
average fixed cost Equal to total fixed cost divided by output (FC/Q).
average variable cost Equal to total variable cost divided by output (VC/Q).
average total cost Equal to total cost divided by output (TC/Q). Average total cost is also equal to AFC + AVC.
Economists refer to total fixed costs divided by output (FC/Q) as average fixed cost (AFC). This represents the average amount of overhead for each unit of output. Total variable costs divided by output is known as average variable cost (AVC). It represents the labor and raw materials expenses that go into each unit of output. Adding AFC and AVC together results in average total cost (ATC), and thus the equation above can be rewritten as
ATC = AFC + AVC
Hence, average cost per unit (ATC) is the sum of average fixed cost (AFC) and average variable cost (AVC).
Average total cost is an important piece of information for firms. Specifically, it provides a general measurement of productivity—how cost-efficient a firm is in producing a specified number of units. Further, it provides the firm guidance as to whether it is earning a profit or whether it should shut down the business and leave the industry altogether.
Returning to Table 3, columns (6), (7), and (8) provide the average fixed cost, average variable cost, and average total cost, respectively, for each quantity of windsurfing sails produced. Let’s calculate the average costs of producing 4 sails. The average fixed cost is calculated by taking the fixed cost of $1,000 and dividing it by 4 to equal $250. Average variable cost takes the variable cost of $1,400 and divides by 4 to equal $350 in AVC. We can calculate average total cost in two ways. First, we can take total cost of $2,400 and divide by 4 sails to equal $600 in ATC. Second, we know that ATC = AFC + AVC, so if we know that AFC is $250 and AVC is $350, then $250 + $350 = $600.
Notice a few trends in the average cost data. First, the average fixed cost falls continuously as more output is produced; this is because your overhead expenses are getting spread out over more and more units of output (this is known as the spreading effect). Figure 2 shows the average fixed cost curve using the data from Table 3. If 2 sails are produced, the average fixed cost is $1,000/2 = $500 (point a on the AFC curve); if 4 sails are produced, the average fixed cost is $1,000/4 = $250 (point b on the AFC curve). Average fixed costs are important to entrepreneurs, who often seek out new businesses with low fixed costs, allowing them to recover these expenses quickly.
FIGURE 2
The Average Fixed Cost Curve The average fixed cost (AFC) curve always decreases as production increases. This is because, in the short run, total fixed costs do not change, so that increasing production spreads the fixed costs over more units of output (the spreading effect).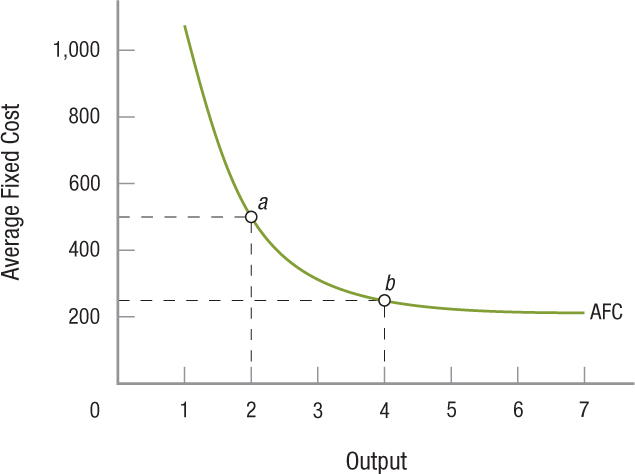
Second, average variable costs and average total costs typically fall initially before rising, just like marginal costs. In the short run, these costs initially fall as the costs of procuring variable inputs fall and due to the spreading effect (which affects the average total cost curve), but these costs eventually rise with greater output as access to available resources dries up, leading to diminishing returns (resulting in a diminishing returns effect). Finally, average variable cost will always be smaller than the average total cost according to the ATC = AFC + AVC equation. These trends will be important as we make greater use of average cost in the next three chapters.
Short-Run Cost Curves for Profit-Maximizing Decisions
Table 3 provides the numerical values for costs. Although all of the costs are important in their own way, we focus on three costs that will provide guidance to firms in their need to maximize profits. These are average variable cost, average total cost, and marginal cost. Let us now translate these costs into figures to make their analysis simpler. Figure 3 shows the three cost measures in graphical form, drawn using the data from Table 3.
FIGURE 3
Average Total Cost, Average Variable Cost, and Marginal Cost The average variable cost (AVC), average total cost (ATC), and marginal cost (MC) curves are shown. The bowl shape of the AVC and ATC curves demonstrates the law of diminishing returns: Beyond a certain level of output, average costs increase. Marginal costs represent the added cost of producing one more unit of output. Note that the marginal cost curve passes through the minimum points on both the AVC and ATC curves.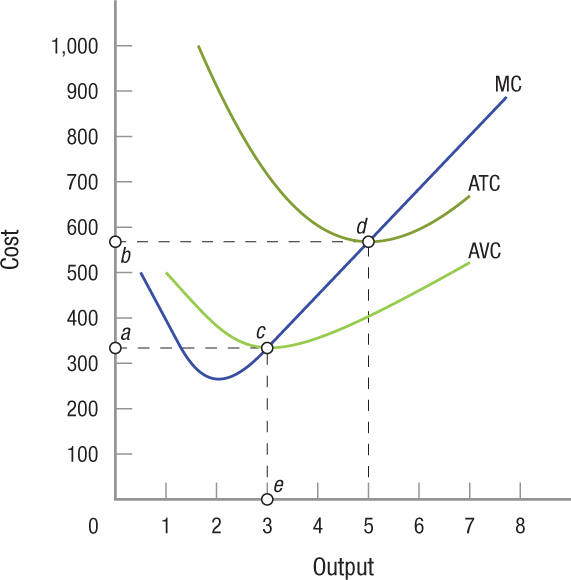
Average Variable Cost (AVC) The AVC and ATC curves are U-shaped. At relatively low levels of output, the curves slope downward, reflecting an increase in returns as average costs drop. As production levels rise, however, diminishing returns set in, and average costs start to climb back up. We get some sense of this by examining Table 3, in which the numbers for AVC and ATC fall and then rise, but the figure makes it far easier to see.
In Figure 3, the average variable cost curve reaches its minimum where 3 sails are produced (point c). Since AVC = VC/Q, then VC = AVC × Q. Thus, at point c, VC is equal to the rectangular area 0ace, or $1,000 ($333.33 × 3).
Average Total Cost (ATC) Average total cost equals total costs divided by output (ATC = TC/Q), or average fixed costs plus average variable cost (ATC = AFC + AVC). In Figure 3, the average total cost reaches its minimum where 5 sails are produced (point d). At this point, the average total cost is $580. As in the previous example, we can calculate the total cost of the firm at any point along the average total cost curve by multiplying the average total cost by the output produced. For example, the total cost of 5 sails would be $580 × 5 = $2,900, exactly as shown in Table 3.
Therefore, the use of cost curves allows us to determine both the total and average costs for a firm, which again is an important component in determining profits. Still, we cannot proceed until we examine marginal costs, a key determinant in whether firms should produce more or less output.
Marginal Cost (MC) Drawing our discussion of short-run costs to a close, Figure 3 plots the marginal cost curve, adding it to the AVC and ATC curves we have plotted already.
Notice that the marginal cost curve intersects the minimum points of both the AVC and ATC curves. This is not a coincidence. Marginal cost is the cost necessary to produce another unit of a given product. When the cost to produce another unit is less than the average of the previous units produced, average costs will fall. For the AVC curve in Figure 3, this happens at all output levels less than 3 units (point c); for the ATC curve, it happens at all output levels less than 5 units (point d). But when the cost to produce another unit exceeds the average cost for all previous output, average costs will rise.
In Figure 3, this happens at output levels greater than 3 units (point c) for AVC and greater than 5 units (point d) for ATC. Over these ranges, marginal cost exceeds AVC and ATC, respectively, and thus the two curves rise. At points c and d, marginal cost is precisely equal to average variable cost and average total cost, respectively, and thus the AVC and ATC curves are at their minimum values (where the slopes are zero).
The average variable cost, average total cost, and marginal cost curves will help us analyze the profit-maximizing equilibrium for each market structure in the next three chapters. We will see how marginal cost provides guidance to firms on the quantity of output to produce, and how average variable cost and average total cost inform firms whether to maintain or expand operations, shut down, or leave the industry.
We have now examined short-run costs for firms when one factor, in this case plant size, is fixed. When this occurs, firms face decisions about whether to operate or shut down given that the fixed costs are paid up front. As we analyze different types of markets in the next three chapters, we will examine how firms make short-run decisions when fixed and variable costs are taken into consideration. Let us now turn to costs in the long run, when all factors, including plant size, are variable. This means that fixed costs do not exist in the long run, because given enough time, a firm can expand or close its plant, and enter or leave an industry.
Long-Run Costs
In the long run, firms can adjust all factor inputs (such as labor and capital) to meet the needs of the market. Here we focus on variations in plant size, while recognizing that all other factors, including technology, can vary.
Figure 4 shows the short-run average total costs curves using three different production functions for three different plant sizes. Plant 1 (ATC1) has fewer machines than either plant 2 or plant 3. With a smaller fixed cost, plant 1 can produce smaller quantities at lower cost than plant 2 or plant 3, which have higher fixed costs. However, if plant 1 tries to increase output, its limited machinery will cause average costs to rise very quickly. For a small output, say Q0, plant 1 produces at an average cost of AC0 (point b). Plant 2, with its additional overhead, can produce Q0 output, but only for a higher average cost of AC2 (point a). And plant 3’s average cost of producing Q0 would be even higher.
FIGURE 4
Various Short-Run Average Cost Curves and the Long-Run Average Total Cost Curve This figure shows the average total cost curve for three plants of different sizes. The larger plants have relatively high average total costs at lower levels of output, but much lower average total costs at higher output levels. Firms are free to adjust plant size in the long run, therefore they can switch from one plant type to the next to minimize their costs at each production level. The green envelope curve represents the firm’s lowest cost to produce any given output in the long run and represents the LRATC curve.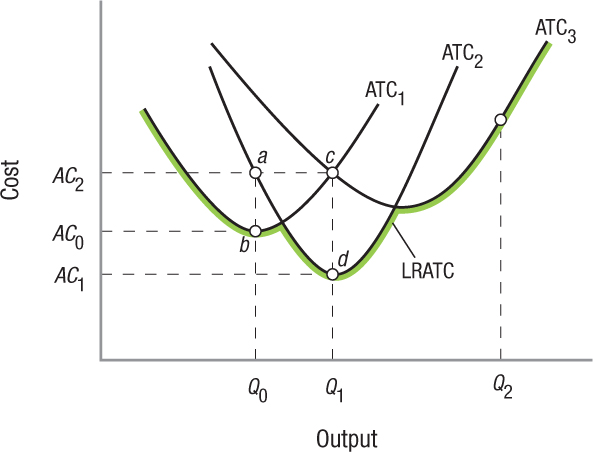
Therefore, at lower levels of production, plant 1 is able to achieve the lowest average cost. However, plant 2 and plant 3 achieve greater cost savings at higher levels of production. Once output rises to Q1, plant 2 begins to enjoy the benefits of a lower average cost of production. The additional machines mean that plant 2 can produce Q1 for AC1 (point d), whereas the machines in plant 1 become overwhelmed at this level of output, resulting in an average cost of AC2 (point c). Similarly, if a firm expects market demand eventually to reach Q2, it would want to build plant 3 because plant 1 and plant 2 are too small to accommodate that level of production efficiently.
long-run average total cost In the long run, firms can adjust their plant sizes so that LRATC is the lowest unit cost at which any particular output can be produced in the long run.
Long-Run Average Total Cost The long-run average total cost (LRATC) curve represents the lowest unit cost at which any specific output can be produced in the long run, when a firm is able to adjust the size of its plant. In Figure 4, the LRATC curve is indicated by the green segments of the various short-run cost curves; these are the segments of each curve at which output can be produced at the lowest per unit cost (also known as the envelope curve, named after its telltale shape). In short, the LRATC assumes that, in the long run, firms will build plants of the size best fitting the levels of output they wish to produce.
Although the LRATC curve in Figure 4 is relatively bumpy, it will tend to smooth out as more plant size options are considered. In some industries, such as agriculture and food service, the options for plant size and production methods are virtually unlimited. In other industries, such as semiconductors, however, sophisticated plants may cost several billion dollars to build and require being run at near capacity to be cost-effective.
These huge, sophisticated plants are so complex that Intel Corporation has dedicated teams of engineers that build new plants and operate them exactly as all others. These teams ensure that any new plant is a virtual clone of the firm’s other operating facilities. Even small deviations from this standard have proven disastrous to cost control in the past.
economies of scale As a firm’s output increases, its LRATC tends to decline. This results from specialization of labor and management, and potentially a better use of capital and complementary production techniques.
Economies and Diseconomies of Scale As a firm’s output increases, its LRATC tends to decrease. This is because, as the firm grows in size, economies of scale result from such items as specialization of labor and management, better use of capital, and increased possibilities for making several products that utilize complementary production techniques.
A larger firm’s ability to have workers specialize in particular tasks reduces the costs associated with shifting workers from one task to another. Similarly, management in larger operations can use technologies not available to smaller firms, for example computers to supervise workers remotely. It is true that today’s powerful personal computer networks have begun to narrow the gap in this arena. Larger firms, though, can still afford to purchase larger, more specialized capital equipment, whereas smaller firms must often rely on more labor-intensive methods. This equipment typically requires large production runs in order to be efficient, and only larger firms can generate the sales necessary to satisfy these production volume requirements. Finally, larger firms are better able to engage in complementary production and use by-products more effectively.
The area for economies of scale is shown in Figure 5 at levels of output below Q0 (average costs are falling).
FIGURE 5
Economies, Diseconomies, and Constant Returns to Scale The curve in this figure shows how increasing production affects long-run average total cost (LRATC). Up to Q0, economies of scale reduce LRATC as production increases. Over the range Q0 to Q1, the firm enjoys constant returns to scale, meaning that it can expand without affecting LRATC. Past Q1, however, diseconomies of scale kick in, such that any further expansion causes an increase in LRATC.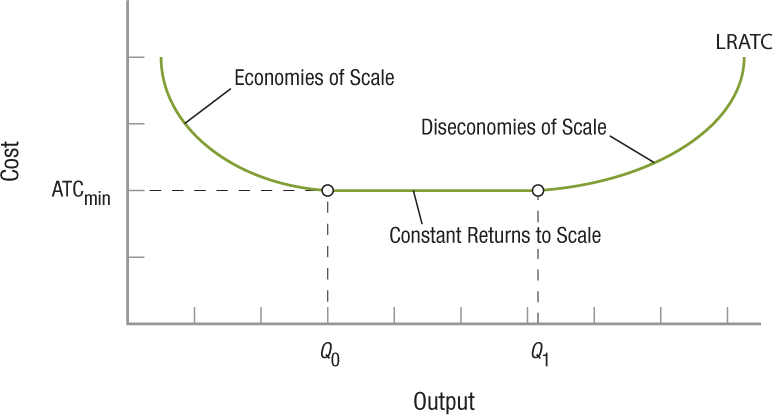
constant returns to scale A range of output where average total costs are relatively constant. The expansion of fast-food restaurant franchises and movie theaters, which are essentially replications of existing franchises and theaters, reflect this.
diseconomies of scale A range of output where average total costs tend to increase. Firms often become so big that management becomes bureaucratic and unable to control its operations efficiently.
In many industries, there is a wide range of output wherein average total costs are relatively constant. Examples include fast-food restaurants, family restaurants such as Outback Steakhouse, and automotive service operations such as Jiffy Lube. Such businesses tend to have steady average costs because the cost to replicate their business in any community is relatively constant. Constructing and running a Dairy Queen franchise, for example, costs roughly the same no matter where it is operated. In Figure 5, this area of constant returns to scale is represented by output levels between Q0 and Q1.
As firms continue to grow, they eventually encounter diseconomies of scale. At some point, the firm gets so big that management is unable to control its operations efficiently. Some firms become so big that they get bogged down in bureaucracy and cannot make decisions quickly. In the late 1980s, Apple fell into this trap—slow to react to changing market conditions for computers and software, the company was left behind by sleeker competition from Dell and Microsoft. Only through downsizing, reorganizing, refocusing, and a management change did Apple get back on track in the late 1990s. Diseconomies of scale—where increased output increases costs disproportionately—are shown at outputs above Q1 in Figure 5.
economies of scope By producing a number of products that are interdependent, firms are able to produce and market these goods at lower costs.
Economies of Scope When firms produce a number of products, it is often cheaper for them to produce another product when the production processes are interdependent. These economies are called economies of scope. For example, once a company has established a marketing department, it can take on the campaign of a new product at a lower cost. It has already developed the expertise and contacts necessary to sell the product. Book publishers can introduce a new book into the market more quickly and cheaply, and with more success than can a new firm starting in the business.
Some firms generate ideas for products, then send the production overseas. After they have been through this process, they become more efficient at it. Economists refer to this as learning by doing. Economies of scope often play a role in mergers as firms look for other firms with complementary products and skills.
Procter & Gamble makes hundreds of household products, taking advantage of large economies of scope by producing many products that use the same inputs and equipment. For example, some of the chemicals used to produce Tide detergent are also used to produce Cascade dishwasher tablets.

Role of Technology We know that technology creates products that were the domain of science fiction writers of the past. Dick Tracy’s wrist radio, first introduced in the comics of 1940s, has now morphed into the many wireless products we see today.
But we should mention in passing the role technology plays in altering the shape of the LRATC curve. The output level at which diseconomies of scale are reached has significantly and continuously expanded since the beginning of the industrial revolution.
Enhanced production techniques, instantaneous global communication, and the use of computers in accounting and cost control are just a few recent examples of ways in which technology has permitted firms to increase their scale beyond what anyone had imagined possible 50 years earlier. Who would have imagined a century ago that one firm could have millions of employees and billions of dollars in annual sales? Today, Wal-Mart has more than two million employees and annual sales of over $500 billion.
How Large Are Fixed Costs? A Look at the Pharmaceutical and Software Industries
We show in this chapter that certain input costs are fixed in the short run, leading to U-shaped average variable and average total cost curves as economies of scale are realized and then exhausted. For most goods and services, economies of scale eventually disappear due to diminishing returns to production, causing average variable and average total costs to rise.
For certain industries, however, fixed costs represent the majority of the total cost of production. Consider the pharmaceutical industry: The cost of developing a successful new drug typically ranges from $100 million to over $1 billion, while the marginal cost of reproducing each pill costs just pennies. The same is true for the software industry; thousands of software engineers spend years writing code, costing the software company millions of dollars to produce the original copy, while the cost of disseminating the software to customers is virtually nothing (if purchased and downloaded online) or a few dollars if nicely packaged on a disc.
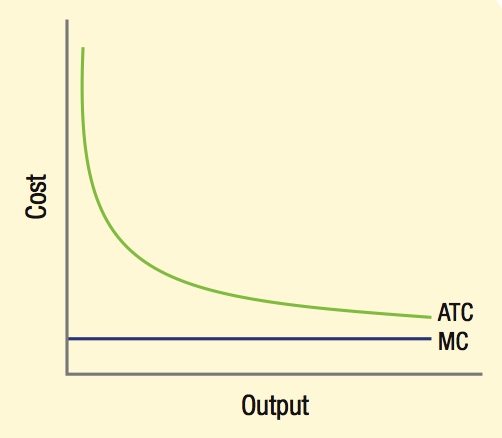
In both cases, the fixed cost of producing a new product far outweighs its variable cost, leading to marginal and average cost curves that differ from the typical U-shaped curves we have seen thus far. Because the marginal cost of reproduction is virtually nothing in these industries, the marginal cost curve for these goods will be horizontal and close to $0. As a result, the average total cost curve will be nearly identical to the average fixed cost curve, which slopes downward as more units are produced.
From this, we see that some products do not follow the typical shape of cost curves. However, these are the exceptions to the rule. Most products continue to show U-shaped marginal and average total cost curves, which are representative of goods that have both fixed and nonnegligible variable costs in their production.
What spurs firms and entrepreneurs to develop new technologies and bring new products to market? Three things: profits, profits, and profits. In this chapter, we analyzed where profits come from by looking at what firms do, how they measure profits, and how they determine production and costs. In the next chapter, we will look at revenues, as well as examine how firms can maximize their profits by adjusting output to market demand.
COSTS OF PRODUCTION
- Fixed costs (overhead) are those costs that do not vary with output, including lease payments and insurance. Fixed costs occur in the short run—in the long run, firms can change plant size or even exit an industry.
- Variable costs rise and fall as a firm produces more or less output. These variable costs include raw materials, labor, and utilities.
- Total cost equals fixed cost plus variable cost (TC = FC + VC).
- Average fixed cost, average variable cost, and average total cost provide a general measure of efficiency when looking at the total amount of output produced.
- Marginal cost is the change in total cost divided by the change in output (MC = ΔTC/ΔQ). Marginal cost provides important information to firms deciding whether to produce more or less output.
- The long-run average total cost curve (LRATC) represents the lowest unit cost at which specific output can be produced in the long run.
- As a firm grows in size, economies of scale result from specialization of labor and better use of capital, while diseconomies of scale occur because a firm gets so big that management loses control of its operations and the firm becomes bogged down in bureaucracy.
- Economies of scope result when firms produce a number of interdependent products, so it is cheaper for them to add another product to the line.
- Modern communications and computers have permitted firms to become huge before diseconomies are reached.
QUESTION: In the late 1990s, Boeing reported that it took roughly 12 years and $15 billion to bring a new aircraft from the design stage to a test flight. Boeing signed a 20-year exclusive agreement to supply aircraft to Delta, American, and Continental (now United) Airlines. The rationale for the agreement was that every time production of the plane doubled, the average production cost per plane would fall by about 20%.5 Why would doubling production cut costs per unit by 20%?
This immense $15 billion development cost is spread over more planes, and rising volume creates economies. Producing commercial aircraft has huge economies of scale and scope.