Nonlinear Relationships
It would be nice for model builders if all relationships were linear, but that is not the case. It is probably not really the case with the amount of studying and GPA either. Figure APX-8 depicts a more realistic nonlinear and positive relationship between studying and GPA. Again, we assume that one can get a D average (1.0) without studying and reach a maximum of straight As (4.0) with 30 hours per week.
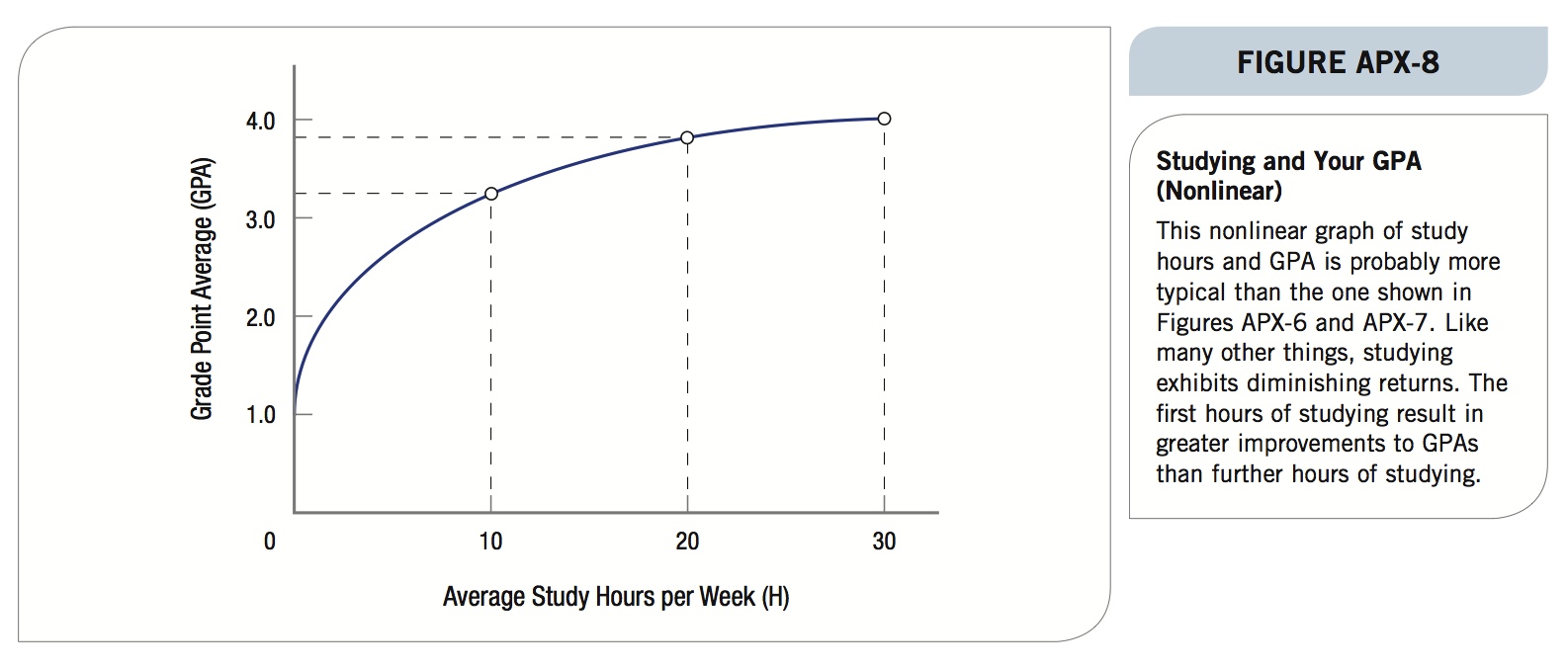
Figure APX-8 suggests that the first few hours of study per week are more important to raising GPA than are the others. The first 10 hours of studying yields more than the last 10 hours: One goes from 1.0 to 3.3 (a gain of 2.3), as opposed to going only from 3.8 to 4.0 (a gain of only 0.2). This curve exhibits what economists call diminishing returns. Just as the first bite of pizza tastes better than the 100th, so the first 5 hours of studying brings a bigger jump in GPA than the 25th to 30th hours.
Computing the Slope of a Nonlinear Curve
As you might suspect, computing the slope of a nonlinear curve is a little more complex than for a linear line. But it is not that much more difficult. In fact, we use essentially the same rise over run approach that is used for lines.
Looking at the curve in Figure APX-8, it should be clear that the slope varies for each point on the curve. It starts out very steep, then begins to level out above 20 hours of studying. Figure APX-9 on the next page shows how to compute the slope at any point on the curve.
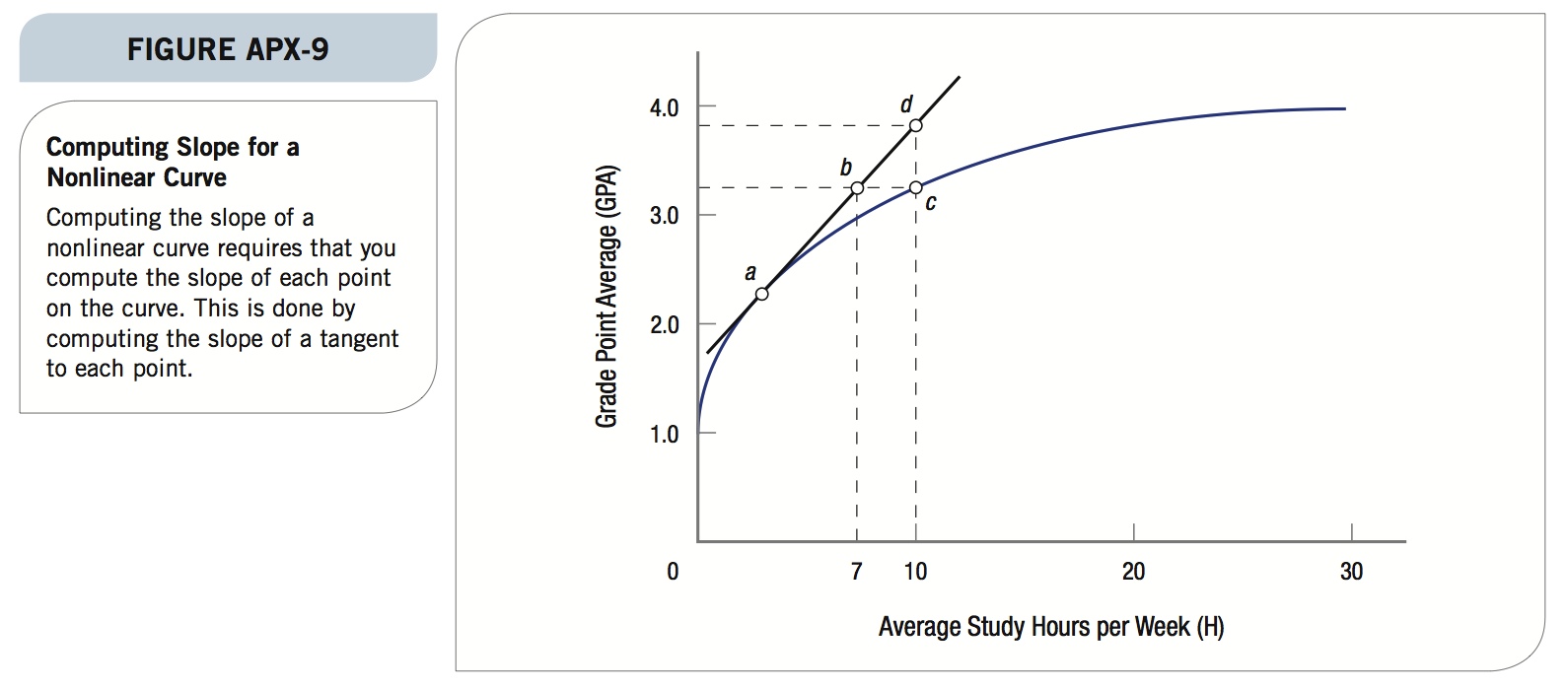
Computing the slope at point a requires drawing a line tangent to that point, then computing the slope of that line. For point a, the slope of the line tangent to it is found by computing rise over run again. In this case, it is length dc ÷ bc or [(3.8 − 3.3) ÷ (10 − 7)] = 0.5 ÷ 3 = 0.167. Notice that this slope is significantly larger than the original linear relationship of 0.1. If we were to compute the slope near 30 hours of studying, it would approach zero (the slope of a horizontal line is zero).