261

Technology is constantly changing. Compare your current smartphone with your previous one and notice the features that have become standard, such as voice recognition typing and advanced GPS applications. Behind the scenes, technology firms such as Apple and Samsung engage in fierce competition in the development of the next technological feature. But developing a new feature itself is not enough; to become the industry standard, all firms must adopt compatible features. Meanwhile, competing firms strive to improve upon existing features to avoid becoming obsolete and losing market power. The study of how oligopoly firms use strategies to gain market power and their effects on both competing firms and consumers form the foundation of game theory.

Game theory is the study of how individuals and firms make strategic decisions to achieve their goals when other parties or factors can influence that outcome. In short, it is the study of strategy and strategic behavior and is used in any situation in which one must consider the possible actions of others and respond by choosing among more than one strategy, each resulting in a potentially different outcome. Although game theory was first developed from the analysis of imperfect competition, particularly in explaining the actions of firms that are oligopolies, today it is used to study situations that extend well beyond the typical economic problems we have seen thus far in this book.

Real-life applications of game theory are abundant, and include situations common in sports coaching, business pricing, management, politics and elections, law and courtroom proceedings, military strategy, and even games such as poker. In 1995 Johnnie Cochran successfully defended O. J. Simpson against a murder charge when the evidence seemed to be stacked against him. In 2008 Barack Obama surpassed favorite Hillary Clinton to become his party’s presidential nominee and eventually the president. In 2011 Google launched its Google+ social media service to challenge Facebook, but ultimately Mark Zuckerberg of Facebook prevailed in maintaining a dominant market share over Google+. As these events suggest, the importance of strategic thinking is a reason why game theory is an interdisciplinary topic that extends well beyond economics.

This section highlights key concepts of game theory, beginning with the important concept of a Nash equilibrium, named after famous mathematician-turned-economist and eventual Nobel Prize winner John Nash. In the next section, we extend this analysis to realistic cases and applications to illustrate how game theory is a part of our lives. We will see how game theory helps explain the actions of oligopolies.

262

The basic setup of a “game” requires players, information, strategies, outcomes, and payoffs. This game setup applies to virtually all situations in which strategy (game theory) is used to analyze a real-life scenario. Let’s look at each component.

In addition to identifying the setup described above, analyses of situations involving game theory typically make two general assumptions:

Game theory moves can be simultaneous or sequential. Simultaneous-move games involve actions by players that occur at the same time. Examples include sporting matches such as a soccer game with offensive and defensive players, and business pricing where firms must decide on prices to be placed in ads without knowing what prices their competitors will choose. Sequential-move games are situations in which one player at a time makes a move. Examples include games such as chess or tic-tac-toe, but also extend to examples such as negotiations (where offers are made back and forth), golf, or reality show competitions.

263

The analysis of simultaneous-move and sequential-move games differs. We’ll begin by briefly discussing how sequential-move games are analyzed, and then proceed to a more in-depth analysis of simultaneous-move games, which are more common in everyday decision making. The next section will then provide additional applications of game theory using both sequential-move and simultaneous-move game analysis.

Sequential-move games are analyzed using a game tree (also known as a decision tree or extensive form analysis). Figure 6 illustrates a game tree with two players, Virgin Galactic and SpaceX, deciding whether or not to continue pursuing a commercial space flight program. Because Virgin Galactic is closer to commercial space flight than SpaceX, it would make the first move, illustrated in the first node with two branches, each specifying a strategy choice. After Virgin makes its choice, SpaceX will then decide whether to pursue its program, knowing what Virgin has decided. The four possible outcomes each correspond to a set of payoffs in parentheses, where the first number is Virgin’s payoff and the second number is SpaceX’s payoff.

The solution to the game tree is found by analyzing how SpaceX responds to Virgin’s strategies and then working backward. If Virgin chooses to pursue, SpaceX’s best response is to pull back; but if Virgin pulls back, SpaceX’s best response is to pursue (because 90 > 10). Being able to predict how SpaceX will respond to each of Virgin’s moves, Virgin then chooses its best outcome, which is to pursue (because 100 > 40). Therefore, the equilibrium in this sequential-move game would be Virgin pursuing the commercial space program with SpaceX pulling back. Although the resulting payoff of 100 for Virgin and 60 for SpaceX is not the best payoff for SpaceX, it is the best it can do given Virgin’s decision. In this game, Virgin has an advantage by moving first. Not all games have a first-mover advantage. For example, in a game of golf, it’s often better to move last, because one can gain valuable information from observing the other players’ shots.

Figure 7 illustrates a two-player simultaneous-move game in a diagram called a game table (also known as a payoff matrix or normal form analysis). In our example, Lowe’s and Home Depot must choose one of two policies: advertise in the local paper or don’t advertise. Lowe’s strategies are listed in rows, while Home Depot’s strategies are listed in columns. Because players (firms) move at the same time, outcomes are determined by the interaction of strategies chosen by each player. In this case, four potential outcomes exist, with Lowe’s payoff shown before Home Depot’s payoff in each outcome box. The final outcome depends on which strategy each player actually chooses.

264

Let’s go through each outcome, to show you how to read the figure. If Lowe’s and Home Depot both advertise, each will earn a profit of $100,000. The advertising will induce some customers to buy now, but won’t much affect whether they will buy at Lowe’s or at Home Depot. There is a cost to advertising, which is why profits are lower when both firms advertise than when both do not. When both do not advertise, each earns a profit of $200,000. Customers continue to go to Lowe’s and Home Depot about equally, and both firms do not bear the cost of the advertising.

What happens if one advertises while the other does not? The one that advertises increases profits. If Lowe’s advertises while Home Depot does not, it earns a profit of $300,000 compared to Home Depot’s payoff of $50,000. Why this result? Lowe’s has to pay the cost of advertising, but more than makes up for it by taking customers away from Home Depot. By not advertising, Home Depot saves on this cost, but it does not make up for the loss of customers. This result is the same, but reversed, if Lowe’s does not advertise while Home Depot does: Home Depot sees $300,000 in profit while Lowe’s profit is only $50,000.

Strategically, what is each firm’s best strategy: Advertise or not advertise? Let’s first look at the best possible outcome for Lowe’s. Its best outcome would be to advertise when Home Depot does not, allowing Lowe’s to earn $300,000 while Home Depot ends up at its worse outcome, earning only $50,000. Alternatively, the best collective outcome for Lowe’s and Home Depot occurs when both do not advertise and each earns $200,000. Is either of these outcomes likely?

Let’s approach this question by looking at the best response of one firm to the other’s action. Suppose Home Depot strives for its highest possible outcome of $300,000 by advertising. What would be Lowe’s best response? Clearly, Lowe’s does not want to bear the minuscule profits of $50,000 if it does not advertise when Home Depot does advertise; therefore, it advertises and earns $100,000. Thus, choosing to advertise is a best response if competitors advertise. In Figure 7, this payoff is underlined.

Looking at this game from Home Depot’s point of view, it also advertises in response to Lowe’s advertising, because it too would not want Lowe’s to grab too many of its customers. Advertising is a best response for Home Depot because it results in a payoff of $100,000 (underlined) instead of $50,000. If both Lowe’s and Home Depot act strategically by advertising to avoid the worst possible outcome, then the best-case scenario of earning $300,000 is not possible.

If the best outcome is not possible, then how about the best collective outcome in which both firms choose not to advertise and each earns $200,000? Clearly, this outcome is better than if both firms advertise. But they cannot call each other up and say, “I will not advertise if you do not advertise.” This is collusion, prevented by law in many countries. Each firm has to make a decision without knowing what the other will do.

Again using the best-response approach, if Home Depot chooses not to advertise, Lowe’s would still be better off advertising, because (1) it eliminates the worst-case outcome if Home Depot does, in fact, advertise, and (2) if Home Depot does not advertise, advertising would allow Lowe’s to achieve its highest payoff of $300,000. Therefore, Lowe’s best response to Home Depot not advertising is still to advertise (the corresponding payoff is underlined in Figure 7). From Home Depot’s perspective, its best response if Lowe’s does not advertise would be to advertise as well.

265

In sum, the best action each firm can take, considering each of the possible actions the other might take, is to advertise. This outcome is what economists call a Nash equilibrium.

A Nash equilibrium occurs when all players in a game use an optimal strategy in response to all other players’ strategies. It is the outcome that maximizes all players’ expected payoffs (the value of each potential outcome times the probability of that outcome occurring) given the information they have. In other words, aiming for the outcome with the highest payoff is not always prudent if the likelihood of achieving that outcome is small. Solving for Nash equilibrium is therefore valuable because it represents a player’s best payoff taking into account the self-interested actions of all other players affecting the outcome. Once a Nash equilibrium is achieved, no individual player can do better by changing his or her mind.

For example, it is possible that Lowe’s or Home Depot could see higher profits if it chose not to advertise, but there’s a higher probability of it leading to lower profits. Nash equilibrium guides players to choose strategies that result in the best expected payoff. In the Lowe’s–Home Depot example, the Nash equilibrium is for each to advertise when neither knows what the other will do.

An outcome is a Nash equilibrium if it results from all players acting strategically (using a best response) to each other’s actions. In some cases, players choose the same action regardless of what others do, while in other cases, players choose different actions in response to other players’ actions. In the Home Depot–Lowe’s example, each firm’s best response is to advertise regardless of what the other firm does, and is known as a dominant strategy. A dominant strategy occurs when one player chooses the same action regardless of what the other player chooses. When both players have a dominant strategy, a single Nash equilibrium will result. For Lowe’s and Home Depot, both advertising is the Nash equilibrium. But not all Nash equilibria are the result of dominant strategies. In fact, games need not be limited to one Nash equilibrium. When dominant strategies do not exist, games can have no Nash equilibrium while others might have more than one, as we’ll soon see.

Also, a Nash equilibrium outcome is not always obvious. In Figure 7, it might seem that Lowe’s and Home Depot not advertising would be a Nash equilibrium; besides, the profits for both are higher than the profits with advertising. But such a quick conclusion does not take into account the fact that one firm could do even better by advertising if the other does not. And because neither firm wishes to risk the worst-case scenario, they both engage in advertising as their best-response action. Fortunately, not all Nash equilibrium outcomes are so pessimistic. In many cases, acting in response to another player’s actions can lead to a good outcome for all players, as we’ll see next.

Nash Equilibrium: A Personal Example Let’s look at a personal example to make sure that the idea of a Nash equilibrium is clear. Suppose you are meeting a classmate to study for an upcoming exam. You didn’t exchange phone numbers, but plan to meet at the local Starbucks tonight. As you head out, you realize that there are two Starbucks near campus: one north of campus and one south. And your classmate also came to the same realization. Without the ability to communicate with your classmate, which location do you choose?

In this scenario, assuming both you and your classmate are making strategic decisions to achieve the same objective, there are four potential outcomes, illustrated in Figure 8. Two of the four outcomes result in a successful meeting, while two result in a missed encounter. In this example, two outcomes meet the criteria for a Nash equilibrium, which is common for coordination-type games when players are attempting to achieve a mutually beneficial outcome. In each Nash equilibrium, both players used strategic thinking to achieve a good outcome. But not so fast! There are actually two Nash equilibria. How would you know which one is the “correct” outcome? Here lies the challenge of this game. Although “Nash equilibrium” describes the outcomes when both players use a best-response strategy, it doesn’t say anything about how to narrow it down to just one outcome. Therefore, players need to use focal points, which are clues that point to a greater likelihood of a successful meeting. The following Issue describes focal points in greater detail.

266

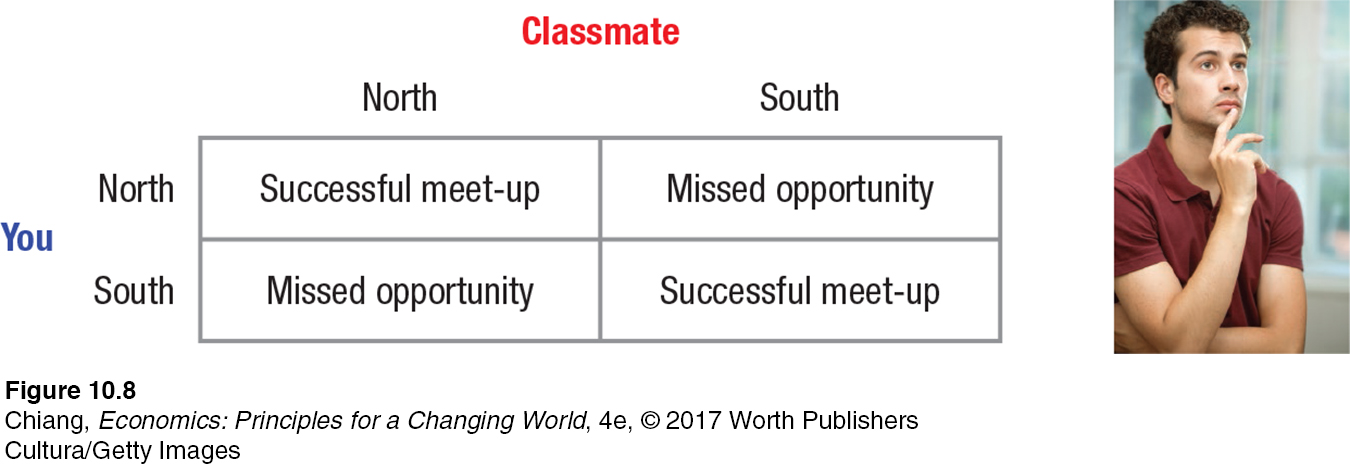
To review, a Nash equilibrium describes any outcome when all players respond optimally to all possible actions by other players. At that outcome, no player would choose to deviate unilaterally from that outcome; this doesn’t mean that a better outcome might prevail with some cooperation, but rather that no player would change her position by herself. Finding a Nash equilibrium is therefore useful because it represents the best outcome given the self-interested actions of all other players.

We have seen two situations with different Nash equilibrium outcomes. For Lowe’s and Home Depot, the Nash equilibrium was an outcome that neither firm truly desired. In the next section, we will classify these outcomes as a Prisoner’s Dilemma and show what can be done to overcome such outcomes. For the study session coordination problem, we found more than one Nash equilibrium in which both players would be happy. But we need not stop here. The next section will highlight other Nash equilibrium outcomes that can result depending on the circumstances facing each player. Because the Nash equilibrium in each situation is not automatically obvious, it’s important to use the best-response method to solve for the Nash equilibrium to ensure that each player’s expected payoff is maximized.

267