chiangmacro4e

Graphs and Data

The main forms of data graphs are time series, scatter plots, pie charts, and bar charts. Time series, as the name suggests, plot data over time. Most of the figures you will encounter in publications are time series graphs.

Time Series

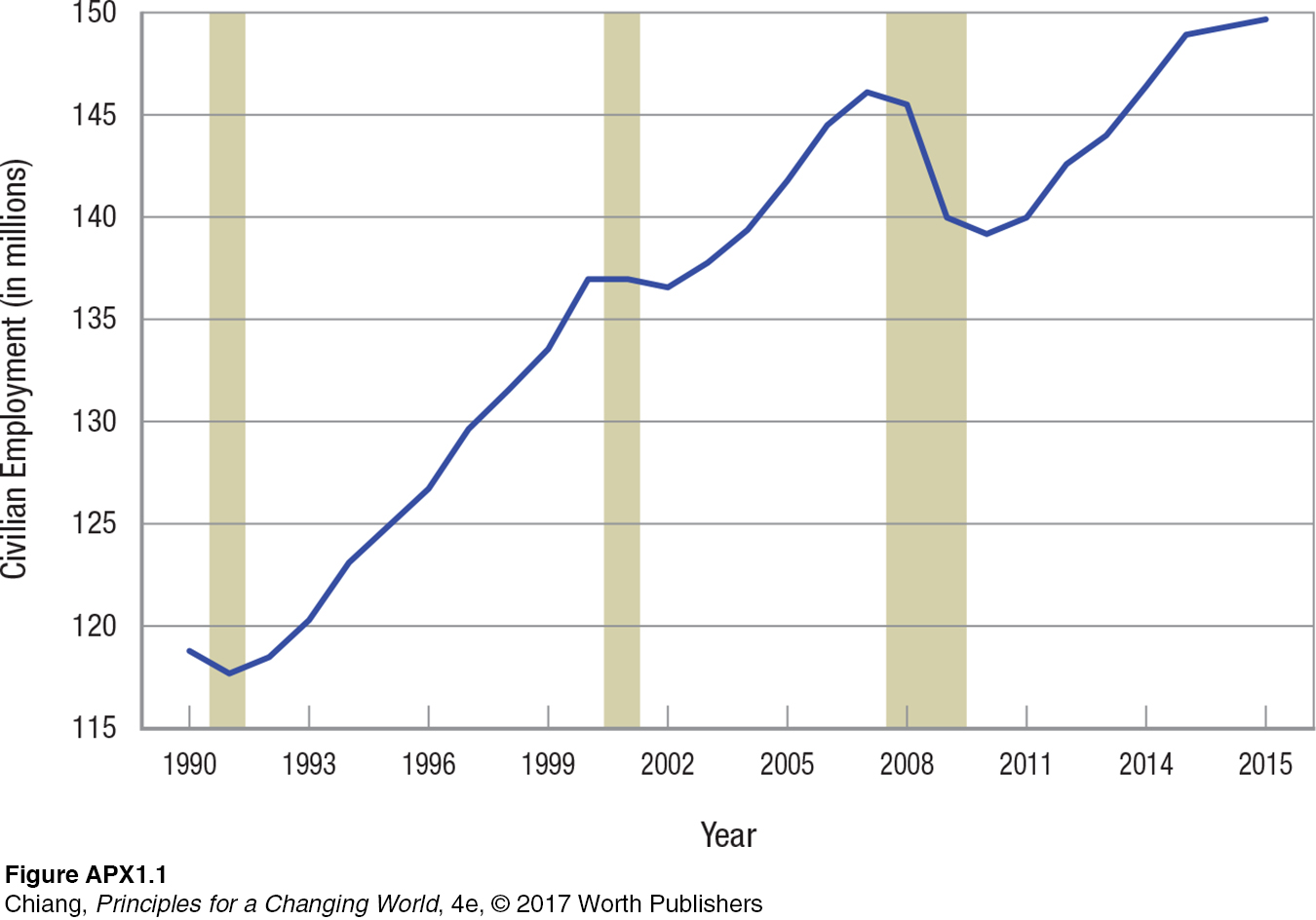
Time series graphs involve plotting time (minutes, hours, days, months, quarters, or years) on the horizontal axis and the value of some variable on the vertical axis. Figure APX-1 illustrates a time series plot for civilian employment of those 16 years and older. Notice that since the early 1990s, employment has grown by almost 25 million for this group. The vertical strips in the figure designate the last three recessions. Notice that in each case when the recession hit, employment fell, then rebounded after the recession ended.

Figure 1.1: FIGURE APX-1 CIVILIAN EMPLOYMENT, 16 YEARS AND OLDER

Figure 1.1: This time series graph shows the number of civilians 16 years and older employed in the United States since 1990. Employment has grown steadily over this period, except in times of recession, indicated by the vertical strips. Note that employment fell during the recession, and then bounced back after each recession ended.

Scatter Plots

Scatter plots are graphs in which two variables (neither variable being time) are plotted against each other. Scatter plots often give us a hint if the two variables are related to each other in some consistent way. Figure APX-2 plots one variable, median household income, against another variable, percentage of Americans holding a college degree.

Figure 1.2: FIGURE APX-2 THE RELATIONSHIP BETWEEN THE MEDIAN HOUSEHOLD INCOME AND THE PERCENTAGE OF AMERICANS HOLDING A COLLEGE DEGREE

Figure 1.2: This scatter diagram plots the relationship between median household income and the percentage of Americans holding a college degree. Median household income increased as a greater proportion of Americans earn college degrees. Note that the percentage of Americans earning college degrees has increased significantly in the last half-century.

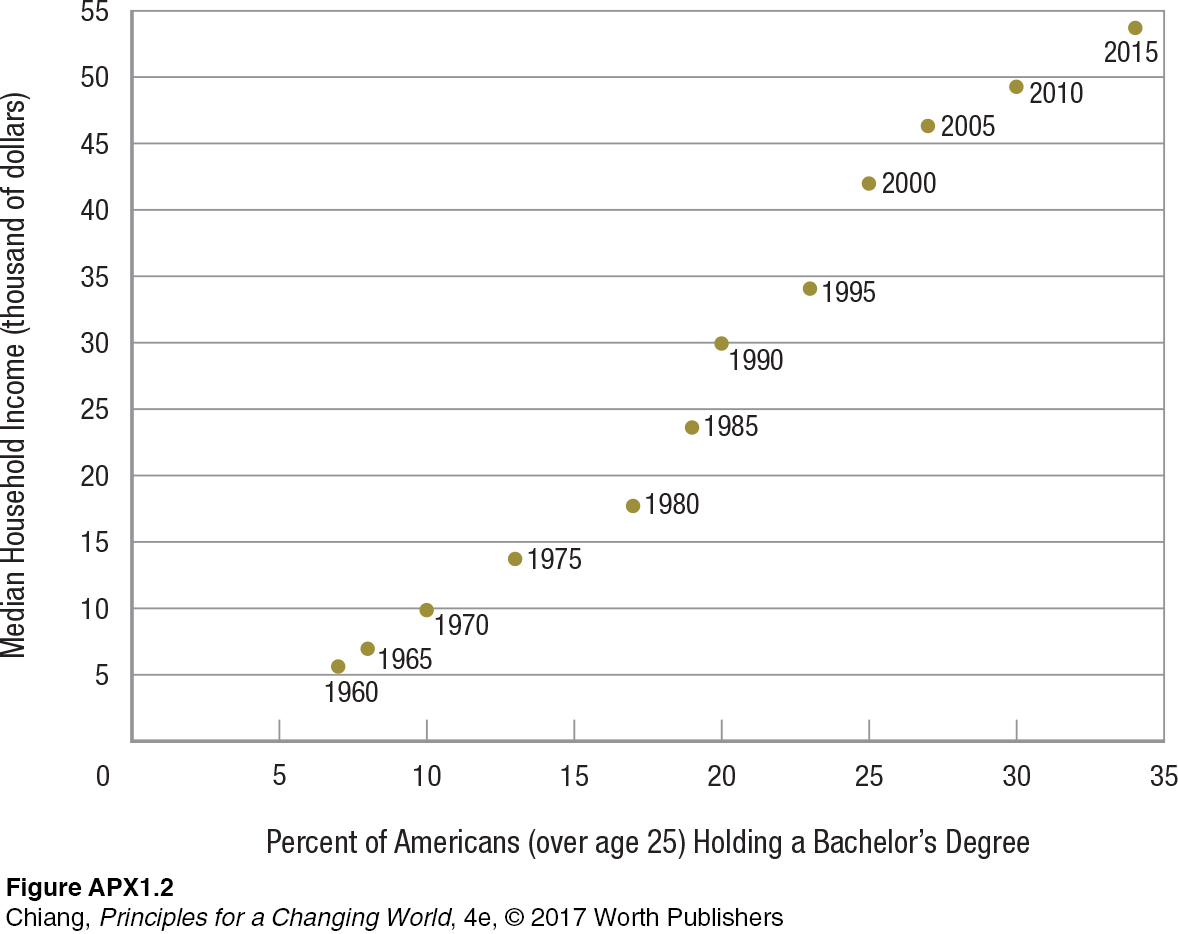
Two things can be seen in this figure. First, these two variables appear to be related to each other in a positive way. A rising percentage of college graduates leads to a higher median household income. It is not surprising that college degrees and earnings are related, because increased education leads to a more productive workforce, which translates into more income. Second, given that the years for the data are listed next to the dots, we can see that the percentage of the population with college degrees has risen significantly over the last half-century. From this simple scatter plot, we can see a lot of information and ideas about how the two variables are related.

Pie Charts

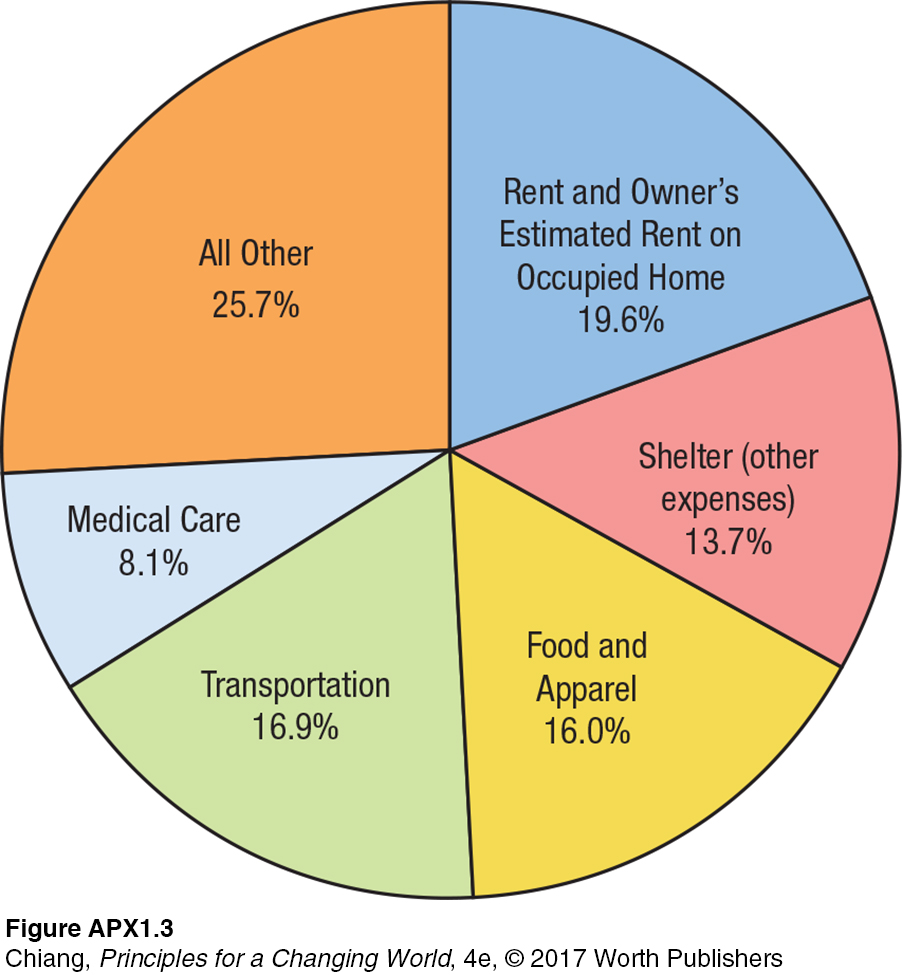
Pie charts are simple graphs showing data that can be split into percentage parts that combined make up the whole. A simple pie chart for the relative importance of components in the consumer price index (CPI) is shown in Figure APX-3. It reveals how the typical urban household budget is allocated. By looking at each slice of the pie, we see a picture of how typical families spend their income.

Figure 1.3: FIGURE APX-3 RELATIVE IMPORTANCE OF CONSUMER PRICE INDEX (CPI) COMPONENTS (2015)

Figure 1.3: This pie chart shows the relative importance of the components of the consumer price index, showing how typical urban households spend their income.

Bar Charts

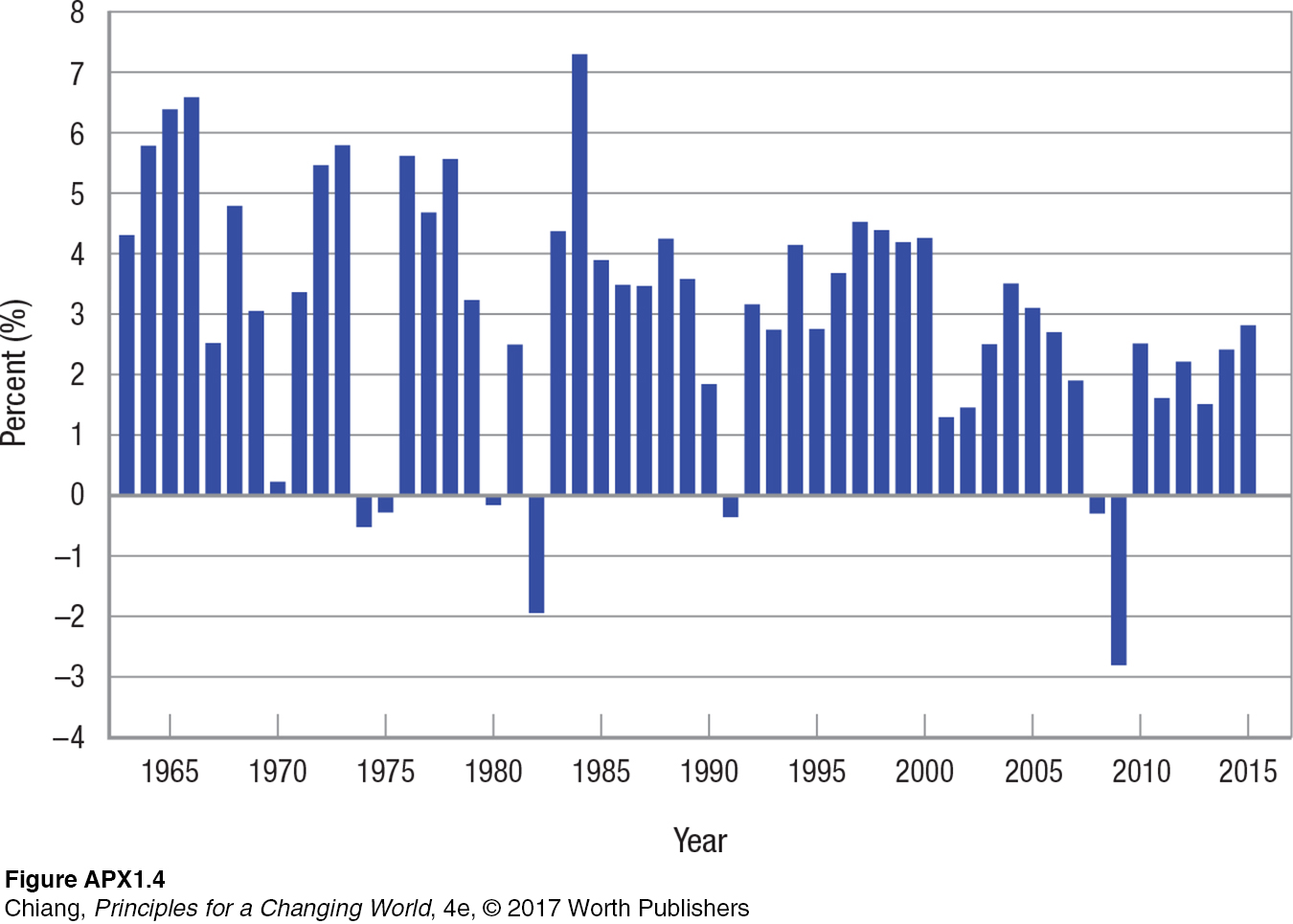
Bar charts use bars to show the value of specific data points. Figure APX-4 is a bar chart showing the annual changes in real (adjusted for inflation) gross domestic product (GDP). Notice that over the last 50 years, the United States has had only 7 years when GDP declined.

Figure 1.4: FIGURE APX-4 PERCENT CHANGE IN REAL (INFLATION ADJUSTED) GDP

Figure 1.4: This bar chart shows the annual percent change in real (adjusted for inflation) gross domestic product (GDP) over the last 50 years. Over this period, GDP declined only 7 times.

Simple Graphs Can Pack In a Lot of Information It is not unusual for graphs and figures to have several things going on at once. Look at Figure APX-5, illustrating the number of social media users as a percent of each age group. On the horizontal axis are the age groups in years. On the vertical axis is the percent of each age group that regularly used social media. Figure APX-5 shows the relationship between age and social media penetration for different periods. They include the most recent period shown (August 2015), a year previous (August 2014), and eight years ago (August 2007).

Figure 1.5: FIGURE APX-5 SOCIAL MEDIA USAGE ACROSS AGE GROUPS

Figure 1.5: These curves show the percentage of Americans using a social media site by age. The curves slope downward because older Americans are less likely to use social media than younger Americans. However, over time, more Americans in all age groups are using social media, as evidenced by each point on the August 2014 curve being higher than the corresponding point on the August 2007 curve, and each point on the August 2015 curve being higher than the corresponding point on the August 2014 curve.

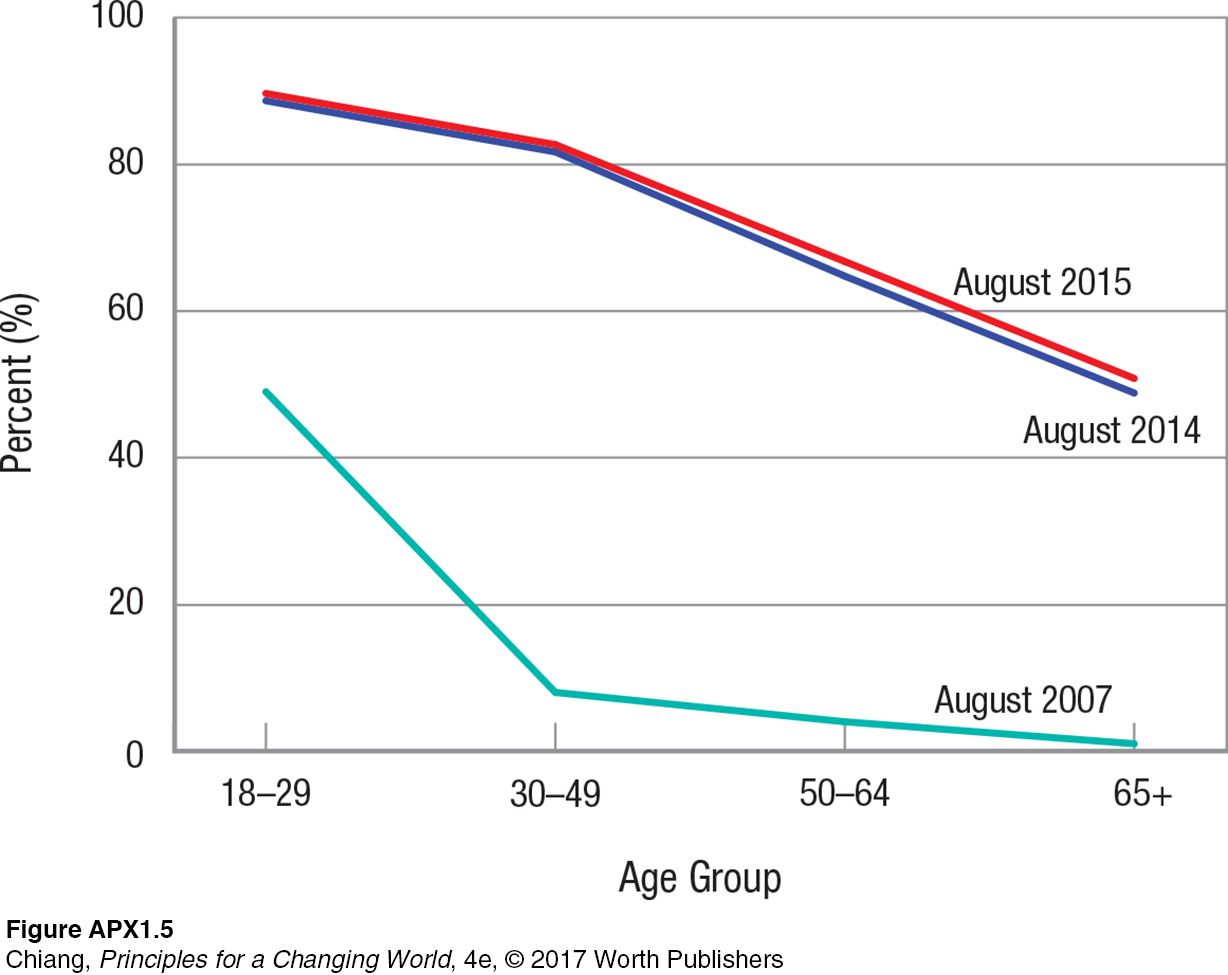
You should notice two things in this figure. First, the relationship between the variables slopes downward. This means that older Americans are less likely to use social media than younger Americans. Second, use of social media has increased across all ages over the three periods studied (from August 2007 to August 2014 to August 2015) as shown by the position of the curves. Each point on the August 2015 curve is above the corresponding point on the August 2014 curve, which is subsequently above each point on the August 2007 curve.

A Few Simple Rules for Reading Graphs Looking at graphs of data is relatively easy if you follow a few simple rules. First, read the title of the figure to get a sense of what is being presented. Second, look at the label for the horizontal axis (x axis) to see how the data are being presented. Make sure you know how the data are being measured. Is it months or years, hours worked or hundreds of hours worked? Third, examine the label for the vertical axis (y axis). This is the value of the variable being plotted on that axis; make sure you know what it is. Fourth, look at the graph itself to see if it makes logical sense. Are the curves (bars, dots) going in the right direction?

Look the graph over and see if you notice something interesting going on. This is really the fun part of looking closely at figures both in this text and in other books, magazines, and newspapers. Often, simple data graphs can reveal surprising relationships between variables. Keep this in mind as you examine graphs throughout this course.

One more thing. Graphs in this book are always accompanied by explanatory captions. Examine the graph first, making your preliminary assessment of what is going on. Then carefully read the caption, making sure it accurately reflects what is shown in the graph. If the caption refers to movement between points, follow this movement in the graph. If you think there is a discrepancy between the caption and the graph, reexamine the graph to make sure you have not missed anything.