This section focuses on four common categories of games: Prisoner’s Dilemma, repeated games, leadership games, and chicken games. In each of the examples within each category, we solve for a Nash equilibrium using the best-response method introduced in the previous section, and discuss the characteristics of these outcomes that are found in real-life examples. In doing this, you should get a sense of how game theory helps explain many oligopoly behaviors.

Ever notice how competing stores pay very close attention to what their competitors do? When Office Depot offers back-to-school specials, Staples is sure to do the same. When one airline offers a summer fare sale, other airlines tend to follow. In our example of Lowe’s and Home Depot in the previous section, each firm chooses to advertise even if it results in lower profits than if neither advertises. If you were a manager of one of these firms, shouldn’t you immediately cease advertising? Not necessarily. Game theory helps to explain this seemingly counterintuitive outcome. In each of these situations, the Nash equilibrium that results is an outcome that is inferior to another outcome that can be achieved through cooperation, and is referred to as a Prisoner’s Dilemma.

Given the similarities of products sold by monopolistically competitive and oligopoly firms, Prisoner’s Dilemma outcomes occur frequently as firms compete for market share, such as AT&T and Verizon in wireless communications, Carnival and Royal Caribbean in cruise vacations, and Target and Walmart in discount retailing.

268

For consumers, however, Prisoner’s Dilemma outcomes are beneficial because they result in lower prices for goods. As competing firms lower their prices to gain market share, they earn a smaller profit from each customer. In some cases, competition becomes so intense that a competitor is forced out of business. Just ask Circuit City, Borders, Sharper Image, and Linens-N-Things, just to name a few. Why would firms compete to the point of nearly zero profit margins? Wouldn’t it make sense for competing firms to utilize their collective market power by all raising their prices to make more money?

Alas, here’s the dilemma: Firms cannot openly collude to raise prices (that is illegal under antitrust laws). However, firms can silently collude by raising prices unilaterally and hoping that others will follow. But will the others follow?

Suppose two shoe stores operate near campus, Shoe Carnival and Shoe Festival. Assume, for simplicity, that each has two pricing strategies: a high markup and a low markup. If both stores choose the same strategy, they each attract the same number of customers. But if one store is less expensive than the other, it takes most of the customers and profits (despite earning less profit per customer at the lower price). Figure 9 shows a game table with presumed profits under the four outcomes.

Using the best-response method to solve for Nash equilibrium, Shoe Carnival’s best response to a high price by Shoe Festival is to price low ($52,000 > $45,000), thereby stealing most of Shoe Festival’s customers and earning a higher profit. And to prevent the same from happening if Shoe Festival prices low, Shoe Carnival’s best response is also to price low ($28,000 > $13,000). Therefore, Shoe Carnival has a dominant strategy to keep its prices low regardless of what Shoe Festival does. In Figure 9, the strategies selected by Shoe Carnival in response to each strategy by Shoe Festival are underlined. If we conduct the same analysis for Shoe Festival, we also find that Shoe Festival has a dominant strategy to price low, resulting in a Nash equilibrium when both stores price low, resulting in a payoff of $28,000 for Shoe Carnival and $25,000 for Shoe Festival.

Does this equilibrium seem odd? It might because another outcome (where both stores price high) provides greater profit to both stores. Yet, that outcome is not a Nash equilibrium. A Prisoner’s Dilemma therefore results because players are unable to cooperate effectively with one another. Why don’t the stores just agree to price their products high? They can’t do it by colluding; that is illegal. And if one store raises its prices unilaterally, there is no guarantee the other store will follow, thus risking a loss of customers and profit.

The Classic Prisoner’s Dilemma How did the Prisoner’s Dilemma get its name? Two criminal suspects (say, Matthew and Chris) are apprehended on a charge of robbery. They are separated, put in solitary confinement, are unable to speak to each other, and are not expected to meet each other even after the prison term is finished. Each prisoner is offered the same bargain: Confess that you and your partner both committed the crime and you will go free while your non-confessing partner will go to prison for three years. If neither confesses, the state likely will convict them both on lesser charges, resulting in a one-year sentence for each. Finally, if both confess, they each will go to prison for two years.

269

Figure 10 illustrates this game in which payoffs represent the number of years in prison. The prisoners must make a decision without knowing what the other chose, and decisions are irrevocable. Each prisoner is only concerned with his own welfare—minimizing his time in prison. Is there a unique solution?

Using the best-response method, Matthew and Chris both have a dominant strategy to confess! This outcome results despite the fact that both would be better off by not confessing: one year served in prison versus two. The Prisoner’s Dilemma results because neither player trusts the other not to confess given the structure of the payoffs.

Other Examples of Prisoner’s Dilemma Outcomes Now that you have an idea of what a Prisoner’s Dilemma entails, particularly when oligopoly firms compete, let’s mention a few other examples in which a Prisoner’s Dilemma might occur.

Resolving the Prisoner’s Dilemma Prisoner’s Dilemma type of situations are difficult to resolve in a noncooperative framework when the players are not able to coordinate their strategies, whether as a result of antitrust laws or an inability to retaliate against other players if the cooperative action is not played. Although Prisoner’s Dilemma outcomes might be bad for firms in a pricing game or for litigants in a trial, they surely are beneficial for consumers who enjoy lower prices and for lawyers who might earn a lot of money in a high-profile case.

270

Let’s consider a case of trade protection in which a Prisoner’s Dilemma might be resolved successfully. A Prisoner’s Dilemma occurs when countries enact trade barriers, causing the gains from trade to be restricted. Free trade agreements are a way for countries to overcome the Prisoner’s Dilemma by agreeing to promote free trade among members. And unlike collusive agreements between firms, free trade agreements are legal and have been implemented extensively in recent decades.

Another way to overcome the Prisoner’s Dilemma is by ensuring that the game is repeated over time. When games are played just once, players have an incentive to maximize their payoffs in the game without worrying about long-term consequences. However, when a game is repeated indefinitely, incentives change, and players worry about retaliation.

Pick up a Sunday newspaper and notice the large selection of circulars included. Many retailers advertise their products using a Sunday ad without knowing what their competitors’ ads look like. But because this game is repeated every Sunday, no firm would risk retaliation by advertising prices that are too low relative to other firms. Thus, repeated games provide a way for competing players to check how other players are behaving, and to provide a way of punishing unfair players.

Games can be endlessly (infinitely) repeated or repeated for a specific number of rounds. In either case, repeating opens the game to different types of strategies that are unavailable for a game played only once. These strategies can take into account the past behavior of rivals. This section briefly explores such strategies and some of their implications for understanding oligopoly behavior.

One possibility is simply to cooperate or defect from the beginning. These strategies, however, leave you at the mercy of your opponent, or lead to unfavorable outcomes where both firms earn less or suffer losses. A more robust set of strategies are trigger strategies, where action is taken contingent on your opponent’s past decisions. Here are a few of them.

Grim Trigger Let’s start by considering an industry that is earning oligopoly profits. Suppose that all of a sudden, one firm lowers its price, maybe because it is in financial trouble and wants to increase sales right away. Under the grim trigger rule, the other firms lower their prices—but they do not stop there. They permanently lower their prices, making the financial condition of the original firm that reduced prices even more severe.

Any decision by your opponent to defect (choose an unfavorable outcome) is met by a permanent retaliatory decision forever. This grim trigger is a harsh decision rule. Moreover, misinterpretation of a player’s actions can result. For example, has your competition lowered its price in an attempt to gain market share at your expense, or has the market softened for the product in general? This strategy can quickly lead to the unfavorable Prisoner’s Dilemma result. To avoid this problem, oligopoly firms might use other trigger strategies.

Trembling Hand Trigger A trembling hand trigger strategy allows for a mistake by your opponent before you retaliate. This gives your opponent a chance to make a mistake and reduces misreads that are a problem for the grim trigger strategy. This approach can be extended to accept two nonsequential defects, and so on, but they can be exploited by clever opponents who figure out that they can get away with a few “mistakes” before their opponent retaliates.

Tit-for-Tat A tit-for-tat strategy is one that repeats the prior move of competitors. If one firm lowers its price, its rivals follow suit one time. If the same firm offers discounts or special offers, rivals do exactly the same in the next time period. This strategy has efficient qualities in that it rewards cooperation and punishes defection.

This short list of strategies illustrates the richness of repeated games. Strategies tend to be more successful if they are relatively simple and easy to understand by competitors, tend to foster cooperation, have some credible punishment to reduce defections, and provide for forgiveness to avoid the costly mistakes associated with misreading opponents.1

1 Nick Wilkinson, Managerial Economics: A Problem Solving Approach (Cambridge, U.K.: Cambridge University Press), 2005, p. 373.

271

Using Sequential-Move Analysis to Model Repeated Games Because repeated games involve multiple iterations of the same game, it can be shown in the sequential-move game tree described in the previous section. In Figure 11, a game tree is shown between two hardware firms that advertise each week in the Sunday ads. To avoid the Prisoner’s Dilemma, both firms must choose to advertise lightly. They continue to do so unless one firm chooses to advertise heavily, which would lead to a trigger strategy in the next stage. Suppose Tool Shack contemplates advertising heavily this week: Tool Kingdom can respond to this action by advertising heavily next week, or choose not to. In the figure, Tool Shack makes the first decision whether to advertise lightly or heavily. If Tool Shack chooses to advertise heavily, Tool Kingdom then chooses whether to respond.

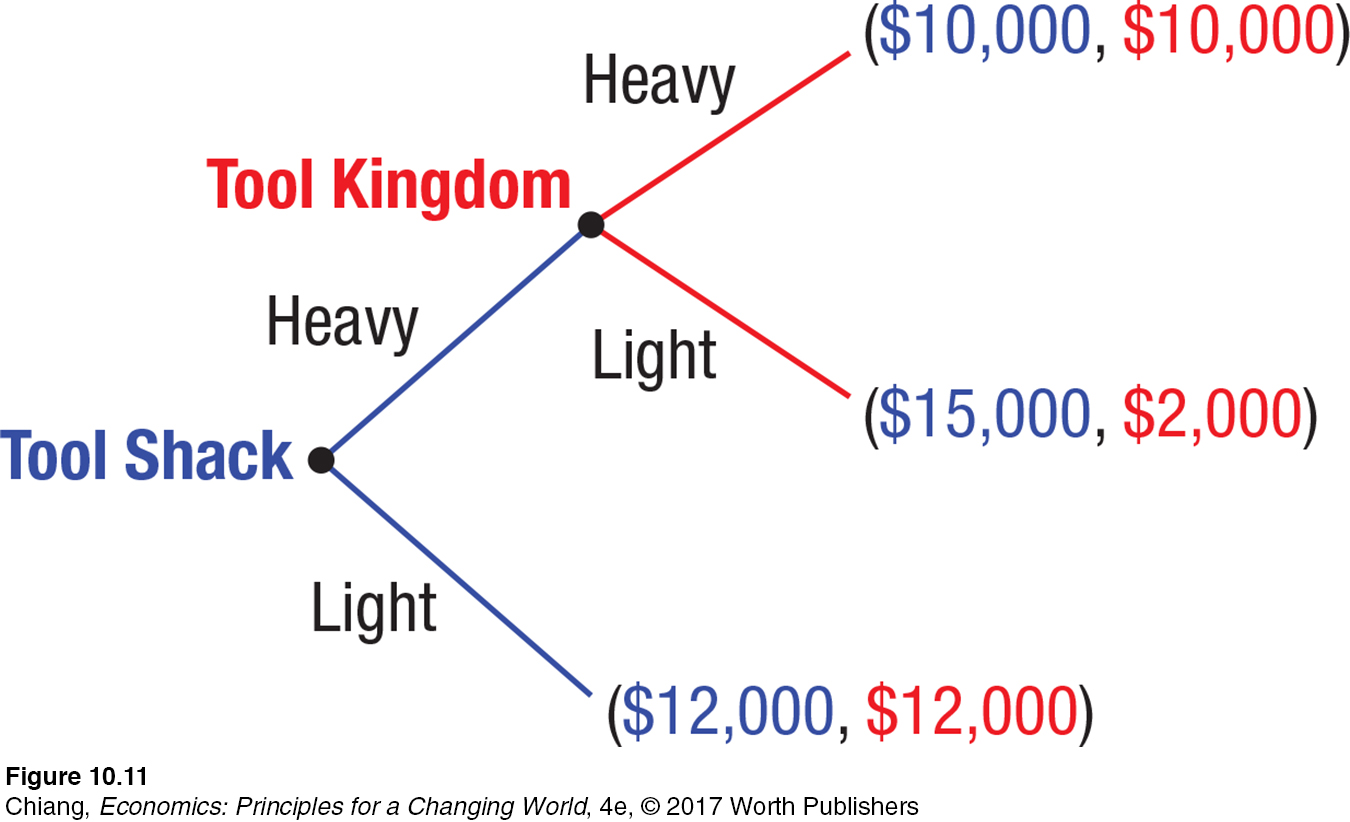
Looking at Tool Kingdom’s payoffs, it is in its best interest to advertise heavily if Tool Shack chooses to advertise heavily. Tool Shack, knowing that advertising heavily would be Tool Kingdom’s best response in the next stage, would likely choose to maintain its light advertising to avoid the Prisoner’s Dilemma outcome. The sequential nature of game trees allows players to see the progression of moves across time from start to finish.

Resolving the Prisoner’s Dilemma is an important outcome of cooperative strategies. But not all competitive games lead to a Prisoner’s Dilemma. One example is called a leadership game, where an industry is dominated by a market leader.

Facebook is the world’s largest social media provider, which earns its revenues primarily through advertising and sets prices to maximize its profits. Yet, other smaller social networks also compete for revenues. Unlike earlier examples, in which competing firms are of similar size, Facebook’s market dominance allows it to ignore the pricing actions of its smaller competitors. In other words, if Facebook loses a few advertisers due to lower prices on other networks, the loss in revenues is smaller than what it would lose if Facebook lowered its prices.

Another example of a leadership game occurs when a small low-fare airline competes against a larger airline. Frontier Airlines is a relatively small airline based in Denver; it competes on many routes that United Airlines serves. But because United is a significantly larger airline with greater market power, it does not always match Frontier’s lower fares because United believes it would not lose many customers.

Another category of game that does not result in a Prisoner’s Dilemma can be seen where collective bargaining (organized labor) is powerful, such as labor unions and unions for professional sports. Every once in a while, a labor dispute reaches a point where a strike is either threatened or sometimes carried out. Although we discuss labor disputes in the next chapter, this is an example of an important class of games called chicken.

272

A chicken game is portrayed in the classic movie Rebel Without a Cause, in which James Dean’s character is challenged by a rival to a stunt challenge. Both players race their cars toward a cliff, and the first person to jump out is the “chicken.” The winner is the person who stays in the car longer. Of course, if neither player leaves his car, they both plunge to their deaths.

Chicken games describe games of holdouts or brinkmanship. Players involved in chicken games want to hold out as long as they can to win, trying to get the other side to give in. If neither side does, the worst outcome occurs. Examples of brinkmanship occur regularly in Congress. Neither Democrats nor Republicans wish to concede anything up to the very end, when some catastrophic consequence threatens the economy such as a government default (from failing to raise the debt ceiling) or a fiscal cliff of higher taxes and severe spending cuts (from failing to agree on a budget). Brinkmanship often ties one’s hands.

Figure 12 illustrates a chicken game using the 2012 NHL labor dispute as an example. The players union and the team owners were in a dispute over salaries. Each side can remain tough, or loosen their position. The worst outcome occurs when both sides refuse to give in, resulting in a lockout or strike that is devastating to both sides, not to mention all the fans, who are not able to watch their favorite teams play.

Using the best-response method, we find that chicken games have two Nash equilibria, where one side ultimately gives in to the other. Specifically, if NHL owners choose the tough strategy by refusing to compromise, the best response of players would be to loosen their position and earn a payoff of 1 instead of 0. If NHL owners are willing to compromise, the best response of players would be to maintain a tough position and earn a payoff of 4 instead of 2. The same best-response strategies can be determined by the NHL owners in response to the NHL players’ strategies.

Thus, in a chicken game, one party is much happier with a Nash equilibrium result than the other. Yet, the loser still would not have wanted to change its strategy, for doing so unilaterally would result in an even worse outcome. Unfortunately for the NHL, a Nash equilibrium did not occur as both sides refused to give in, resulting in a lockout and a severely compromised 2012–2013 season. This is an outcome that occasionally occurs in chicken games, one that had clear consequences for both players and owners, not to mention many disappointed fans.

As seen in the many applications in this and the last section, game theory is a powerful tool to analyze market competition when firms each have the ability to influence price and the market share of their competitors. The ability to anticipate another player’s actions and respond optimally is the key to achieving a Nash equilibrium. Nash equilibrium is the outcome that maximizes all players’ expected payoffs. Recognizing such outcomes allows all players to achieve the best outcome given the self-interested motives of all other players involved. Game theory has applications that extend beyond oligopoly competition and economics in general.

In this and the previous two chapters, we have studied the four major market structures: perfect competition, monopolistic competition, oligopoly, and monopoly. As we move through this list, market power becomes greater, and the ability of the firm to earn economic profits in the long run grows.

Table 1 summarizes the important distinctions among these four market structures. Keep in mind that market structure analysis allows you to look at the overall characteristics of the market and predict the pricing and profit behavior of the firms. The outcomes for perfect competition and monopolistic competition are particularly attractive for consumers because firms price their products equal to average total costs and earn just enough to keep them in business over the long haul.

273

In contrast, the outcomes for oligopoly and monopoly industries are not as favorable to consumers. Concentrated markets have considerable market power, which shows up in pricing and output decisions. However, keep in mind that markets with market power (oligopolies) often involve giants competing with giants. Even though there is a mutual interdependence in their decisions and they may not always compete vigorously over prices, they often are innovative because of some competitive pressures. We see this today especially in the electronics and automobile markets.