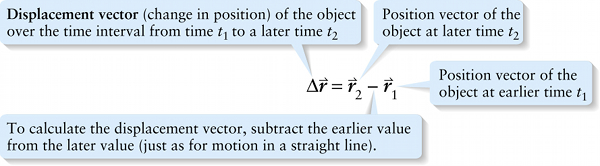
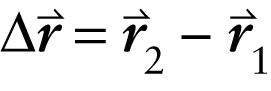Displacement vector equals the change in position vector over time interval (3-6)

Question 1 of 4

Question

To calculate the displacement vector, subtract the earlier value from the later value (just as for motion in a straight line).

{"title":"displacement","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,14,35,53\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"position vector of the object at later time t sub 2","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,17,148,55\"}]"} {"title":"calculate the displacement vector","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"181,21,210,51\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"position vector of the object at earlier time t sub 1","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"224,20,257,53\"}]"}

Question

Position vector of the object at later time $t_2$

{"title":"displacement","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,14,35,53\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"position vector of the object at later time t sub 2","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,17,148,55\"}]"} {"title":"calculate the displacement vector","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"181,21,210,51\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"position vector of the object at earlier time t sub 1","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"224,20,257,53\"}]"}

Question

Position vector of the object at earlier time $t_1$

{"title":"displacement","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,14,35,53\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"position vector of the object at later time t sub 2","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,17,148,55\"}]"} {"title":"calculate the displacement vector","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"181,21,210,51\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"position vector of the object at earlier time t sub 1","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"224,20,257,53\"}]"}

Question

$\textbf{Displacement vector}$ (change in position of the object over the time interval from time $t_1$ to a later time $t_2$

{"title":"displacement","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,14,35,53\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"position vector of the object at later time t sub 2","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,17,148,55\"}]"} {"title":"calculate the displacement vector","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"181,21,210,51\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"position vector of the object at earlier time t sub 1","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"224,20,257,53\"}]"}

Review

This vector points from the object’s position at $t_1$ to its position at $t_2$ , and is the difference between the object’s position vector $\boldsymbol{\vec{r_2}}$ at $t_2$ and its position vector $\vec{r_1}$ at $t_1$ .