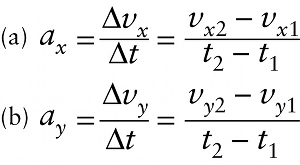Components of the acceleration vector (3-10)

Question 1 of 5

Question

$x$ component of the acceleration vector $\boldsymbol{\vec{a}}$

{"title":"x component of the acceleration vector a","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"49,39,72,64\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"change in the x component of the velocity during a short time interval","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"272,19,301,44\"},{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"}]"} {"title":"change in the y component of the velocity during a short time interval","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"275,91,298,120\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"elapsed time for the time interval","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"257,45,282,70\"},{\"shape\":\"rect\",\"coords\":\"251,130,282,159\"}]"} {"title":"y component of the acceleration vector a","description":"Incorrect","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"51,118,73,142\"}]"}

Question

$y$ component of the acceleration vector $\vec{a}$

{"title":"x component of the acceleration vector a","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"49,39,72,64\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"change in the x component of the velocity during a short time interval","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"272,19,301,44\"},{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"}]"} {"title":"change in the y component of the velocity during a short time interval","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"275,91,298,120\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"elapsed time for the time interval","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"257,45,282,70\"},{\"shape\":\"rect\",\"coords\":\"251,130,282,159\"}]"} {"title":"y component of the acceleration vector a","description":"Correct!","type":"correct","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"51,118,73,142\"}]"}

Question

Change in the $x$ component of the velocity during a short time interval

{"title":"x component of the acceleration vector a","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"49,39,72,64\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"change in the x component of the velocity during a short time interval","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"272,19,301,44\"},{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"}]"} {"title":"change in the y component of the velocity during a short time interval","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"275,91,298,120\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"elapsed time for the time interval","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"257,45,282,70\"},{\"shape\":\"rect\",\"coords\":\"251,130,282,159\"}]"} {"title":"y component of the acceleration vector a","description":"Incorrect","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"51,118,73,142\"}]"}

Question

Change in the $y$ component of the velocity during a short time interval

{"title":"x component of the acceleration vector a","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"49,39,72,64\"},{\"shape\":\"poly\",\"coords\":\"82,133\"}]"} {"title":"change in the x component of the velocity during a short time interval","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"272,19,301,44\"},{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"}]"} {"title":"change in the y component of the velocity during a short time interval","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"275,91,298,120\"},{\"shape\":\"poly\",\"coords\":\"113,132\"}]"} {"title":"elapsed time for the time interval","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"257,45,282,70\"},{\"shape\":\"rect\",\"coords\":\"251,130,282,159\"}]"} {"title":"y component of the acceleration vector a","description":"Wrong","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"51,118,73,142\"}]"}

Review

It’s often useful to express the acceleration vector $\vec{a}$ of an object in terms of its $x$ and $y$ components. Use the symbols $v_{1x}$ and $v_{1y}$ for the velocity components of the object at time $t_1$ , and the symbols $v_{2x}$ and $v_{2y}$ for the velocity components at time $t_2$ . Then $a_x$ , the $x$ component of $\vec{a}$ , equals the $x$ component of velocity change ( $\Delta{v_x} = v_{x2} - v_{x1}$ divided by the time interval $\Delta{t} = t_2 - t_1$ , and the $y$ component of $vec{a}$ equals the $y$ component of velocity change ( $\Delta{v_y} = v_{y2} - v_{y1}$ ) divided by $\Delta{t}$ .