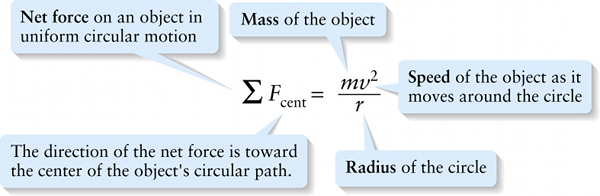
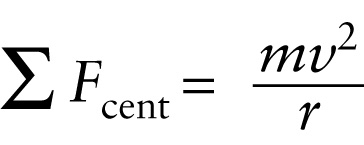Newton's second law equation for uniform circular motion (5-11)
Question 1 of 5
Question
Radius of the cirlce
{"title":"Net force on an object in uniform circular motion","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,43,55,109\"}]"} {"title":"The direction of the net force is toward the center of the object's circular path","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"97,97,169,126\"}]"} {"title":"Mass of the object","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"251,40,306,78\"}]"} {"title":"Speed of the object as it moves around the circle","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"310,36,337,76\"}]"} {"title":"Radius of the circle","description":"Correct!","type":"correct","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"294,98,326,134\"}]"}Review
Because the acceleration is always toward the center of the circle, it follows from Newton’s second law that at any instant the net external force acting on the object of mass m must likewise be directed toward the center of the circle. Furthermore, the magnitude of the net external force must be equal to macent. We can write this statement in equation form as: