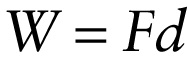Work done by a constant force that points in the same direction as straight-line displacements (6-1)

Question 1 of 3

Question

Magnitude of the constant force $\boldsymbol{\vec{F}}$

{"title":"Work done an object by a constant force vector F that points in the same direction as the object's displacement vector d","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,68,56\"}]"} {"title":"Magnitude of the constant force vector F","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"120,2,156,59\"}]"} {"title":"Magnitude of the displacement vector d","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"157,8,187,60\"}]"}

Question

$\textbf{Work}$ done on an object by a constant force $\boldsymbol{\vec{F}}$ that points in the same direction as the object's displacement $\boldsymbol{\vec{d}}$

{"title":"Work done an object by a constant force vector F that points in the same direction as the object's displacement vector d","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,68,56\"}]"} {"title":"Magnitude of the constant force vector F","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"120,2,156,59\"}]"} {"title":"Magnitude of the displacement vector d","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"157,8,187,60\"}]"}

Question

Magnitude of the displacement $\boldsymbol{\vec{d}}$

{"title":"Work done an object by a constant force vector F that points in the same direction as the object's displacement vector d","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,68,56\"}]"} {"title":"Magnitude of the constant force vector F","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"120,2,156,59\"}]"} {"title":"Magnitude of the displacement vector d","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"157,8,187,60\"}]"}

Review

Suppose a constant force $\vec{F}$ acts on an object as it moves through a straight-line displacement $\vec{d}$ , and the force $\vec{F}$ is in the same direction as $\vec{d}$ . Then the work done by the force equals the product of the force magnitude $F$ and the distance $d$ over which the object moves: