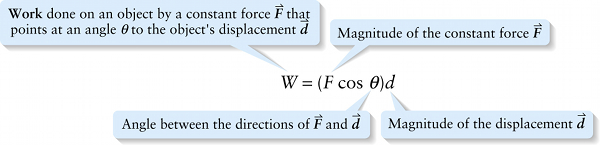
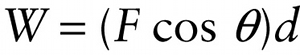Work done by constant force at an angle 0 to the straight-line displacement (6-2)

Question 1 of 4

Question

Angle between the directions of $\boldsymbol{\vec{F}}$ and $\boldsymbol{\vec{d}}$

{"title":"Work done an object by a constant force F that points at an angle theta to the objects displacement vector d","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,47,45\"}]"} {"title":"Magnitude of the constant force vector F","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"115,2,142,48\"}]"} {"title":"Magnitude of the displacement vector d","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"276,4,299,45\"}]"} {"title":"Angle between the directions vector F and vector d","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"231,8,264,44\"}]"}

Question

$\textbf{Work}$ done on an object by a constant force $\boldsymbol{\vec{F}}$ that points at an angle $\theta$ to the object's displacement $\boldsymbol{\vec{d}}$

{"title":"Work done an object by a constant force F that points at an angle theta to the objects displacement vector d","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,47,45\"}]"} {"title":"Magnitude of the constant force vector F","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"115,2,142,48\"}]"} {"title":"Magnitude of the displacement vector d","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"276,4,299,45\"}]"} {"title":"Angle between the directions vector F and vector d","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"231,8,264,44\"}]"}

Question

Magnitude of the constant force $\boldsymbol{\vec{F}}$

{"title":"Work done an object by a constant force F that points at an angle theta to the objects displacement vector d","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,47,45\"}]"} {"title":"Magnitude of the constant force vector F","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"115,2,142,48\"}]"} {"title":"Magnitude of the displacement vector d","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"276,4,299,45\"}]"} {"title":"Angle between the directions vector F and vector d","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"231,8,264,44\"}]"}

Question

Magnitude of the displacement $\boldsymbol{\vec{d}}$

{"title":"Work done an object by a constant force F that points at an angle theta to the objects displacement vector d","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,3,47,45\"}]"} {"title":"Magnitude of the constant force vector F","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"115,2,142,48\"}]"} {"title":"Magnitude of the displacement vector d","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"276,4,299,45\"}]"} {"title":"Angle between the directions vector F and vector d","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"231,8,264,44\"}]"}

Review

How can we calculate the work done by a constant force that is not in the direction of the object’s motion? As an example, in Figure 6-6a a groundskeeper is using a rope to pull a screen across a baseball diamond to smooth out the dirt. The net tension force $\vec{F}$ that the rope exerts on the screen is at an angle with respect to the direction in which the screen moves. In such a case, only the component of the force along the direction of motion contributes to the work done (Figure 6-6b).

If $\theta$ is the angle between the force $\vec{F}$ and the displacement $\vec{d}$ , this component of the force is $F \cos \theta$ . Hence the amount of work done by the force is: