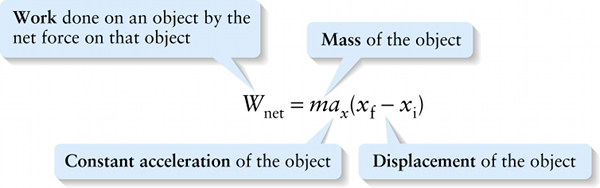
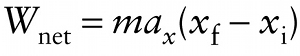Work done by a constant net force, straight-line motion (6-6)
Question 1 of 4
Question
Mass of the object
{"title":"Work done on an object by the net force on that object","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,2,42,35\"}]"} {"title":"Mass of the object","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"111,12,144,37\"}]"} {"title":"Displacement of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"189,12,210,40\"}]"} {"title":"Constant acceleration of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"145,10,166,36\"}]"}Review
Newton’s second law tells us that a ∑Fx=max, where m is the mass of the object. So we can rewrite Equation 6-5 as: