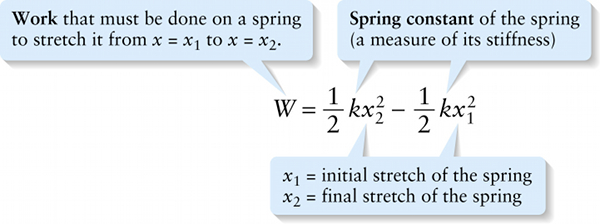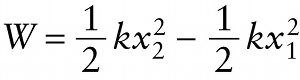Gravitation potential energy (6-14)

Question 1 of 3

Question

$x_1$ = initial stretch of the spring
$x_2$ = final stretch of the spring

{"title":"Work that must be done on a spring to strech it from x = x sub 1 to x = x sub 2","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,13,38,53\"}]"} {"title":"Spring constant of the spring (a measure of its stiffness)","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"114,21,132,53\"},{\"shape\":\"rect\",\"coords\":\"243,19,264,55\"}]"} {"title":"x sub 1 = initial stretch of the spring, x sub 2 = final stretch of the spring","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"132,26,151,52\"},{\"shape\":\"rect\",\"coords\":\"263,31,287,53\"}]"}

Question

$\textbf{Spring constant}$ of the spring (a measure of its stiffness)

{"title":"Work that must be done on a spring to strech it from x = x sub 1 to x = x sub 2","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,13,38,53\"}]"} {"title":"Spring constant of the spring (a measure of its stiffness)","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"114,21,132,53\"},{\"shape\":\"rect\",\"coords\":\"243,19,264,55\"}]"} {"title":"x sub 1 = initial stretch of the spring, x sub 2 = final stretch of the spring","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"132,26,151,52\"},{\"shape\":\"rect\",\"coords\":\"263,31,287,53\"}]"}

Question

$\textbf{Work}$ that must be done on a spring to stretch it from $x = x_1$ to $x = x_2$ .

{"title":"Work that must be done on a spring to strech it from x = x sub 1 to x = x sub 2","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,13,38,53\"}]"} {"title":"Spring constant of the spring (a measure of its stiffness)","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"114,21,132,53\"},{\"shape\":\"rect\",\"coords\":\"243,19,264,55\"}]"} {"title":"x sub 1 = initial stretch of the spring, x sub 2 = final stretch of the spring","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"132,26,151,52\"},{\"shape\":\"rect\",\"coords\":\"263,31,287,53\"}]"}

Review

Figure 6-18 graphs the force that you exert as a function of the distance x that the spring has been stretched. If the spring is initially stretched a distance $x_1$ and you stretch it further to $x_2$ , the work W that you do is equal to the area of the colored trapezoid in Figure 6-18. From geometry, this area is equal to the average height of the graph multiplied by the width $x_2 - x_1$ . Equation 6-12 can be simplified to: