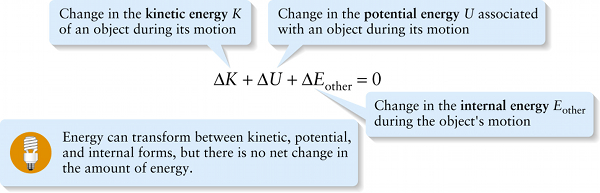
The law of conservation of energy (6-28)
Question
Change in the \(\textbf{kinetic energy}\) \(K\) of an object during its motion
{"title":"Change in the kinetic energy K of an object during its motion","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"20,1,43,34\"}]"} {"title":"Change in the potential energy U associated with an object during its motion","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"98,4,122,28\"}]"} {"title":"Change in the internal energy E sub \perpher during the object's motion","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"158,5,178,31\"}]"}
Review
Equation 6-28 suggests that we broaden our definition of energy to include both total mechanical energy \((E = K + U)\) and internal energy \(E_{\mathrm{other}}\). In this case, we have to expand the system to include not only the object and the sources of the conservative forces that produce \(\Delta{U}\), but also the sources of the nonconservative forces that result in \(\Delta{E}_{\mathrm{other}}\) (like your hand in the case of the thrown pencil). As the object moves, \(K\), \(U\), and \(E_{\mathrm{other}}\) can all change values, but the sum of these changes is zero: One kind of energy can transform into another, but the total amount of energy of all forms remains the same. This is the most general statement of the \(\textbf{law of conservation of energy}\).
