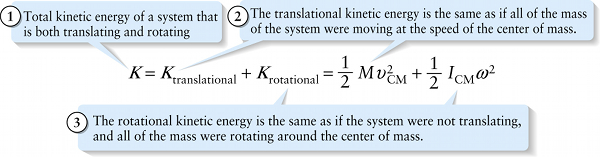
Total kinetic energy for a rigid object undergoing both translation and rotation (8-12)
Question
Total kinetic energy of a system that is both translating and rotating
{"title":"1) Total kinetic energy of a system that is both translating and rotating","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,6,17,25\"}]"} {"title":"2) The translational kinetic energy is the same as if all of the mass of the system were moving at the speed of the center of mass.","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"25,5,43,25\"},{\"shape\":\"rect\",\"coords\":\"187,6,205,25\"}]"} {"title":"3) The rotational kinetic energy is the same as if the system were not translating, and all of the mass were rotating around the center of mass.","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"112,13,161,29\"},{\"shape\":\"rect\",\"coords\":\"268,15,290,30\"}]"}Review
We can also use the principle of conservation of energy for a rigid object that’s both moving through space as a whole and rotating. In such a situation it turns out that we can write the object’s total kinetic energy as the sum of two terms: the translational kinetic energy associated with the motion of the object’s center of mass (see Section 7-7), and the rotational kinetic energy associated with the object’s rotation around its center of mass (Figure 8-12). If the object has mass M and its center of mass is moving with speed vCM, its translational kinetic energy is K=12Mv2CM ; if the object’s moment of inertia for an axis through its center of mass is ICM and it rotates with angular speed ω, its rotational kinetic energy is Krotational=12ICMω2. The total kinetic energy (translational plus rotational) of the object is then: