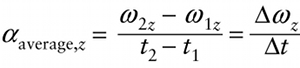Average angular acceleration (8-14)
Question 1 of 3
Question
Elapsed time for the time interval: The object has angular velocity ω1z at time t1, and has angular velocity ω2z at time t2.
{"title":"Average angular acceleration of a rotating object","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,23,21,50\"}]"} {"title":"Change in angular velocity of the object over a certain time interval: The angular velocity changes from omega sub 1z to omega sub 2z","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"159,8,181,22\"},{\"shape\":\"rect\",\"coords\":\"250,5,273,29\"}]"} {"title":"Elapsed time for the time interval: The object has angular velocity omega sub 1z at time t sub 1, and has angular velocity omega sub 2z at time t sub 2.","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"154,41,183,53\"},{\"shape\":\"rect\",\"coords\":\"258,39,281,60\"}]"}Review
Suppose a rigid object is rotating around the z axis with angular velocity ω1z at time t1 and with angular velocity ω2z at a later time t2 (Figure 8-15). The average angular acceleration αaverage,z (the Greek letter α, or alpha) for the time interval between t1 and t2 is the change in angular velocity, Δωz=ω2z−ω1z divided by the duration of the time interval, Δt=t2−t1: