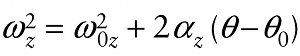Angular velocity, angular acceleration, and angular position for constant angular acceleration only (8-17)
Question
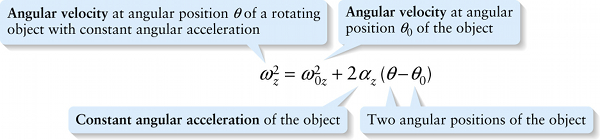
Two angular positions of the object
{"title":"Angular velocity at angular position theta of a rotating object with constant angular acceleration","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"3,18,26,40\"}]"} {"title":"Angular velocity at angular position theta sub 0 of the object","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"74,17,98,43\"}]"} {"title":"Constant angular acceleration of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"173,17,194,42\"}]"} {"title":"Two angular positions of the object","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"221,12,239,43\"},{\"shape\":\"rect\",\"coords\":\"260,13,282,41\"}]"}Review
It’s straightforward to write down the equations for rotational motion with constant angular acceleration. To see how, take a look at the equations for linear velocity vx and angular velocity ωz, and the equations for linear acceleration ax and angular acceleration αz:
| Linear Motion | Rotational Motion | ||
|---|---|---|---|
|
|
(linear velocity) |
|
(angular velocity) |
|
|
(linear acceleration) |
|
(angular acceleration) |
Comparing these equations shows that the rotational quantities θ, ωz, and αz are related to each \perpher in exactly the same way that x, vx, and ax are related to each \perpher. So we can take the equations for constant linear acceleration and convert them to the equations for constant angular acceleration by replacing x with θ, vx with ωz, and ax with αz. The equations for linear motion are:
(2-5) vx=v0x+axt (constant acceleration only)
(2-9) x=x0+v0xt+12axt2 (constant x acceleration only)
(2-11) v2x=v20x+2ax(x−x0) (constant x acceleration only)
Hence, along with equations 8-16 and 8-15, the equation for constant angular acceleration is: