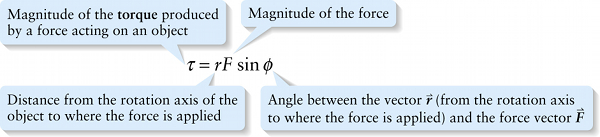
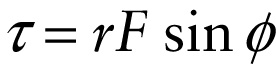Magnitude of torque (8-18)

Question 1 of 4

Question

Magnitude of the $\textbf{torque}$ produced by a force acting on an object

{"title":"Magnitude of the torque produced by a force acting on an object","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,40,53\"}]"} {"title":"Magnitude of the force","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"113,12,151,51\"}]"} {"title":"Angle between the vector r (from the rotation axis to where the force is applied) and the force vector F","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"241,11,277,66\"}]"} {"title":"Distance from the rotation axis of the object to where the force is applied","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"91,16,114,54\"}]"}

Question

Angle between the vector $\vec{r}$ (from the rotation axis to where the force is applied) and the force vector $\vec{F}$

{"title":"Magnitude of the torque produced by a force acting on an object","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,40,53\"}]"} {"title":"Magnitude of the force","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"113,12,151,51\"}]"} {"title":"Angle between the vector r (from the rotation axis to where the force is applied) and the force vector F","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"241,11,277,66\"}]"} {"title":"Distance from the rotation axis of the object to where the force is applied","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"91,16,114,54\"}]"}

Review

Suppose that you exert a force $\vec{F}$ on an object as shown in Figure 8-19a. We use the symbol $\vec{r}$ to denote the vector from the rotation axis to the point where the force is applied, and we use the symbol $\phi$ (the Greek letter phi) for the angle between the directions of $\vec{r}$ and $\vec{F}$ . The component of $\vec{F}$ that points straight out from the rotation axis, $F\ \mathrm{cos}\ \phi$ , doesn’t have any tendency to make the object rotate. But the perpendicular component of $\vec{F}$ , $F\ \mathrm{sin}\ \phi$ , $\textit{does}$ tend to make the object rotate—in this case in a clock-wise direction. We describe the rotational effect of the force $\vec{F}$ by a quantity called the torque $\tau$ (the Greek letter tau) associated with the force. This is given by: