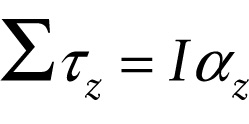Newton's second law of rotational motion (8-20)

Question 1 of 3

Question

The object’s moment of inertia for the axis about which it can rotate

{"title":"The net torque, or sum of all external torques acting on an object for the axis about which it can rotate","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,56,83\"}]"} {"title":"The angular acceleration produced by the net torque","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"197,47,232,86\"}]"} {"title":"The object’s moment of inertia for the axis about which it can rotate","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"166,36,196,81\"}]"}

Review

If torque plays the same role for rotational motion as force plays for translational motion, then we should be able to replace $F_x$ with $\tau_z$ , $m$ with $I$ , and $a_x$ with $\alpha_z$ in Equation 4-4a to get the rotational version of Newton’s second law: