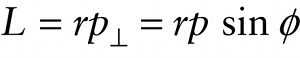Magnitude of the angular momentum of particle (8-23)

Question 1 of 3

Question

Component of the particle’s linear momentum perpendicular to the vector r from rotation axis to particle

{"title":"Magnitude of the angular momentum of a particle","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,2,32,42\"}]"} {"title":"Component of the particle’s linear momentum perpendicular to the vector r from rotation axis to particle","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"88,12,113,46\"},{\"shape\":\"rect\",\"coords\":\"154,37,157,37\"},{\"shape\":\"rect\",\"coords\":\"222,8,271,42\"}]"} {"title":"Distance from the rotation axis to the particle","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,12,190,38\"},{\"shape\":\"rect\",\"coords\":\"69,14,88,39\"}]"}

Review

Figure 8-27 shows that only the component of the momentum $\vec{p}$ that’s perpendicular to $\vec{r}$ contributes to rotation around the axis, so only this component $p_\perp = p \sin{\theta}$ contributes to the angular momentum. We define the magnitude of the angular momentum as: