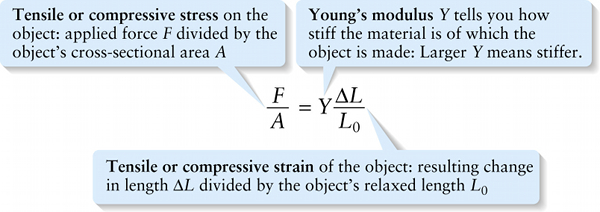
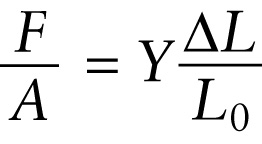Hooke's law for an object under tension or compression (9-3)
Question 1 of 3
Question
Tensile or compressive stress on the object: applied force F divided by the object’s cross-sectional area A
{"title":"Tensile or compressive stress on the object: applied force divided by the object’s cross-sectional area","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,3,59,122\"}]"} {"title":"Young’s modulus tells you how stiff the material is of which the object is made: Larger value means stiffer.","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"137,35,173,85\"},{\"shape\":\"rect\",\"coords\":\"154,37,157,37\"}]"} {"title":"Tensile or compressive strain of the object: resulting change in length divided by the object’s relaxed length","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"220,10,254,55\"}]"}Review
Here’s a useful way to rewrite Hooke’s law for an object under tension or compression. This will also help us define stress and strain more precisely. First we substitute k from Equation 9-2 into Equation 9-1.
F=(YAL0)ΔL
Then we divide both sides by the cross-sectional area A: