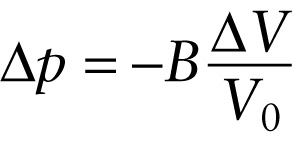Hooke's law for an oject under volume stress (9-6)
Question 1 of 4
Question
Volume stress on the object: change in the pressure p on all sides of the object
{"title":"Volume stress on the object: change in the pressure p on all sides of the object","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"33,45,69,100\"}]"} {"title":"Bulk modulus B: How difficult it is to compress the material of which the object is made; larger B means harder to compress.","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"164,36,200,86\"},{\"shape\":\"rect\",\"coords\":\"154,37,157,37\"}]"} {"title":"Volume strain of the object: resulting change in volume Delta V divided by the object's initial volume v sub 0","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"257,11,291,56\"}]"} {"title":"Important! If ∆p is positive, then ∆V is negative; if ∆p is negative, then ∆V is positive.","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"127,49,167,75\"}]"}Review
In terms of the quantities Δp, V0, and ΔV depicted in Figure 9-10, we can rewrite Equation 9-5 as:
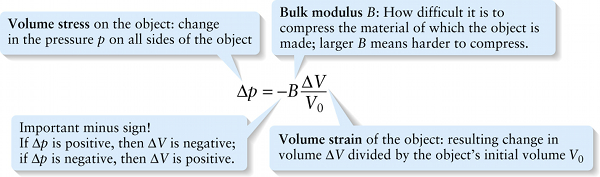
To get more insight into the meaning of Equation 9-6, multiply both sides by −V0/B to rewrite it so that ΔV is by itself on one side of the equation:
9-7 ΔV=−ΔpBV0