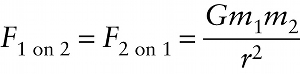Newton's law of universal gravitation (10-2)

Question 1 of 5

Question

Center-to-center distance between the two objects

{"title":"Any two objects exert equally strong gravitational forces on each \perpher.","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,23,28,63\"},{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"102,19,133,60\"}]"} {"title":"Gravitational constant (same for any two objects)","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"201,1,230,32\"}]"} {"title":"Masses of the two objects","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"263,4,289,30\"},{\"shape\":\"rect\",\"coords\":\"231,3,253,33\"}]"} {"title":"Center-to-center distance between the two objects","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"235,52,255,73\"}]"} {"title":"The gravitational forces are attractive: vector F sub 1 on 2 pulls object 2 toward object 1 and vector F sub 2 on 1 pulls object 1 toward object 2.","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"32,40,56,59\"},{\"shape\":\"rect\",\"coords\":\"134,42,156,61\"}]"}

Question

$\textbf{Gravitational constant}$ (same for any two objects)

{"title":"Any two objects exert equally strong gravitational forces on each \perpher.","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,23,28,63\"},{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"102,19,133,60\"}]"} {"title":"Gravitational constant (same for any two objects)","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"201,1,230,32\"}]"} {"title":"Masses of the two objects","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"263,4,289,30\"},{\"shape\":\"rect\",\"coords\":\"231,3,253,33\"}]"} {"title":"Center-to-center distance between the two objects","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"235,52,255,73\"}]"} {"title":"The gravitational forces are attractive: vector F sub 1 on 2 pulls object 2 toward object 1 and vector F sub 2 on 1 pulls object 1 toward object 2.","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"32,40,56,59\"},{\"shape\":\"rect\",\"coords\":\"134,42,156,61\"}]"}

Question

The gravitational forces are attractive: $F_{\mathrm{1\ on\ 2}}$ pulls object 2 toward object 1 and $F_{\mathrm{2\ on\ 1}}$ pulls object 1 toward object 2.

{"title":"Any two objects exert equally strong gravitational forces on each \perpher.","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"1,23,28,63\"},{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"102,19,133,60\"}]"} {"title":"Gravitational constant (same for any two objects)","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"201,1,230,32\"}]"} {"title":"Masses of the two objects","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"263,4,289,30\"},{\"shape\":\"rect\",\"coords\":\"231,3,253,33\"}]"} {"title":"Center-to-center distance between the two objects","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"235,52,255,73\"}]"} {"title":"The gravitational forces are attractive: vector F sub 1 on 2 pulls object 2 toward object 1 and vector F sub 2 on 1 pulls object 1 toward object 2.","description":"Correct!","type":"correct","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"32,40,56,59\"},{\"shape\":\"rect\",\"coords\":\"134,42,156,61\"}]"}

Review

For the force of Earth on the Moon, $m_2$ is the Moon’s mass and $r$ is the Earth-Moon distance. If Equation 10-1 is true for any two objects, then it must also be true that the object of mass $m_2$ exerts a gravitational force on the object of mass $m_1$ , and this force is directly proportional to the mass $m_1$ . But Newton’s third law (Section 4-5) tells us that the forces that the two objects exert on each \perpher have opposite directions and the same magnitude: $F_{\mathrm{2\ on\ 1}} = F_{\mathrm{1\ on\ 2}}$ . Hence the gravitational force that each object exerts on the \perpher must be directly proportional to both $m_1$ and $m_2$ . This chain of reasoning leads us to Newton’s law of universal gravitation: