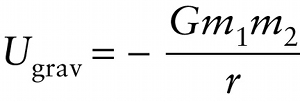Gravitation potential energy (10-4)
Question
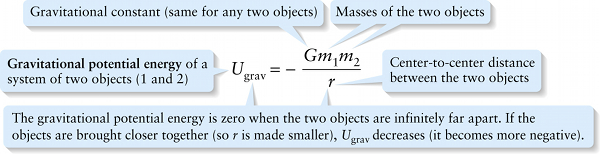
The gravitational potential energy is zero when the two objects are infinitely far apart. If the objects are brought closer together (so r is made smaller), Ugrav decreases (it becomes more negative).
{"title":"Gravitational constant","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"170,2,201,35\"}]"} {"title":"Masses of the two objects","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"204,14,236,39\"},{\"shape\":\"rect\",\"coords\":\"248,11,285,41\"}]"} {"title":"Center-to-center distance between the two objects","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"216,72,248,97\"}]"} {"title":"The gravitational potential energy is zero when the two objects are infinitely far apart. If the objects are brought closer together (so r is made smaller), U sub grav decreases (it becomes more negative).","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"30,59,81,86\"},{\"shape\":\"rect\",\"coords\":\"211,70,250,100\"}]"} {"title":"Gravitational potential energy of a system of two objects (1 and 2)","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"1,30,34,70\"}]"}Review
The expression in Equation 10-4 looks nothing like the familiar formula Ugrav=mgy. To understand the difference, let’s consider two different cases in which gravitational potential energy changes (Figure 10-8).
In Figure 10-8a a woman on Earth’s surface raises a book of mass mbook a vertical distance d. To do this she must work against a gravitational force on the book of magnitude mbookg, and so she must exert an upward force of the same magnitude. So she does an amount of work mbookgd in the process. The book begins and ends at rest, so the work mbookgd that she does goes into increasing the gravitational potential energy associated with the book: ΔUgrav=mbookgd. If the woman stands on a ladder and once again lifts the book by a distance d, the gravitational force she works against is still mbookg since the gravitational force exerted by Earth changes hardly at all near Earth’s surface. So she again does work mbookgd, and the gravitational potential energy increases by the same amount mbookgd as before. As Figure 10-8b shows, this means that the gravitational potential energy increases in direct proportion to the object’s height y, and so the graph of Ugrav versus height is a straight line: Ugrav=mbookgy.
Now imagine the same person has donned a spacesuit and has brought the book with her to a point in space a distance rA from the center of Earth (Figure 10-8c). At this point the gravitational force that Earth exerts on the book has magnitude FA=GmEarthmbook/r2A. If she moves the book an additional distance d away from Earth, she has to exert a force of the same magnitude on the book and so does an amount of work FAd=(Gmbook/r2A)d. Just as on Earth, the work that she does goes into increasing the gravitational potential energy. If she now moves to a greater distance rB from the center of Earth and repeats the process, Earth's gravitational force has a smaller magnitude FB=GmEarthmbook/r2Bd, and so adds a smaller amount of gravitational potential energy. This means that at great distances, the gravitational potential energy does not increase in direct proportion to the distance r and the graph of Ugrav versus distance is not a straight line. Instead, the graph becomes shallower with increasing values of r (Figure 10-8d). This is just what Equation 10-4 tells us, which helps to justify this expression for gravitational potential energy.