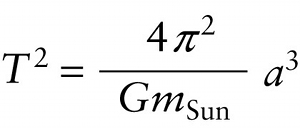Newton's form of Kepler's law of periods (10-16)
Question 1 of 4
Question
Semimajor axis of the object’s orbit
{"title":"Period of an object in an elliptical orbit around the Sun","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,51,33,85\"}]"} {"title":"Semimajor axis of the object’s orbit","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"261,64,287,94\"}]"} {"title":"Mass of the Sun","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"rect\",\"coords\":\"151,91,184,115\"}]"} {"title":"Gravitational constant","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"112,81,149,113\"}]"}Review
The first two of Kepler’s laws describe how a given planet moves in its orbit. His third law, the law of periods, compares the orbital periods of orbits of different sizes:
The square of the period of a planet’s orbit is proportional to the cube of the semimajor axis of the orbit.
This is precisely the relationship that we found for circular orbits in Equation 10-12. Newton was able to show that the law of periods follows from the law of universal gravitation even for elliptical orbits, if we replace the orbital radius r in Equation 10-12 with the semimajor axis a. For objects orbiting the Sun, we must also replace Earth’s mass mEarth with the mass of the Sun: