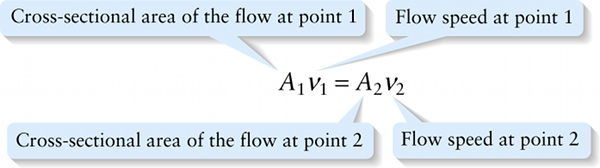
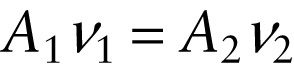Equation of continuity for steady flow of an imcompressible fluid (11-19)

Review

It takes some time interval $\Delta{t}$ for the slug of fluid to enter the region at point 1. And since the volume of fluid between the points must remain constant, the slug of fluid at point 2 must exit the region in the same time interval. If we divide Equation 11-17 by the time interval $\Delta{t}$ it takes for the slugs of fluid to enter or exit the region, we arrive at

$A_1\frac{\Delta{x_1}}{\Delta{t}} = A_2\frac{\Delta{x_2}}{\Delta{t}}$

To see why we divided through by $\Delta{t}$, note that the fluid at point 1 moves a distance $\Delta{x_1}$ during the time interval $\Delta{t}$ and so has speed $v_1 = \Delta{x_1}/\Delta{t}$. SImilarly, the fluid at point 2 (which moves a distance $\Delta{x_2}$ during the same time interval) has speed $v_2 = \Delta{x_2}/\Delta{t}$. So we can rewrite Equation 11-18 as the following relationship called the $\textbf{equation of continuity}$: