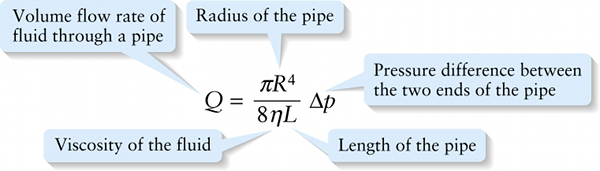
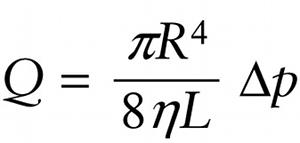Hagen-Poiseuille equation for laminar flow of a viscous fluid (11-30)
Question
Volume flow rate of fluid through a pipe
{"title":"Volume flow rate of fluid through a pipe","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"2,55,51,106\"}]"} {"title":"Radius of the pipe","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"157,18,191,62\"}]"} {"title":"Pressure difference between the two ends of the pipe","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"poly\",\"coords\":\"132,99\"},{\"shape\":\"rect\",\"coords\":\"242,59,271,101\"}]"} {"title":"Length of the pipe","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"181,90,210,134\"}]"} {"title":"Viscosity of the fluid","description":"Incorrect","type":"incorrect","color":"#339966","code":"[{\"shape\":\"rect\",\"coords\":\"149,96,181,141\"}]"}Review
Figure 11-36 shows the laminar flow of fluid within a circular pipe seen in cross section. Due to friction, the fluid that’s right up against the inside walls of the pipe doesn’t move at all. This is the no-slip condition that we described in Section 11-9. (The fluid in contact with the lower plate in Figure 11-34 behaved the same way.) The fluid a small distance from the walls moves a little, the fluid a bit farther away moves a bit faster, and so on. The fastest flow is at the very center of the pipe. This flow pattern is called parabolic (since the dashed curve in Figure 11-36 is a parabola lying on its side). A derivation using calculus gives the following expression, called the Hagen-Poiseuille equation, relating the pressure difference between the two ends of the pipe to the resulting flow rate. (Non-French speakers can pronounce Poiseuille as “pwa-zoo-yah.”)