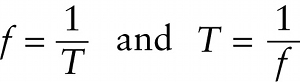Frequency and period (12-1)

Question 1 of 2

Question

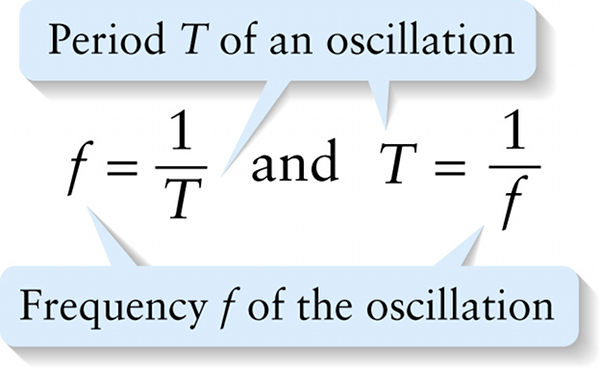
Frequency $f$ of the oscillation

{"title":"Period T of an oscillation","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"56,44,88,76\"},{\"shape\":\"rect\",\"coords\":\"195,18,229,56\"}]"} {"title":"Frequency f of the oscillation","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"1,27,19,60\"},{\"shape\":\"rect\",\"coords\":\"275,46,297,81\"}]"}

Question

Period $T$ of an oscillation

{"title":"Period T of an oscillation","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"56,44,88,76\"},{\"shape\":\"rect\",\"coords\":\"195,18,229,56\"}]"} {"title":"Frequency f of the oscillation","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"1,27,19,60\"},{\"shape\":\"rect\",\"coords\":\"275,46,297,81\"}]"}

Review

To help us understand how a wave propagates over time, imagine a series of “snapshots” of a sinusoidal wave equally spaced in time like the frames of a movie. Figure 13-7 shows such a series. As the wave moves through the medium, an individual piece of the medium (like the blue dot in Figure 13-7) oscillates up and down. Just as in Section 12-2, we use the term period and the symbol $T$ for the time required for each piece of the medium to go through a complete oscillation cycle. Furthermore, just as in Sections 12-2 and 12-3 the frequency $f$ (in hertz, or Hz) is the number of cycles that a piece of the medium goes through per second, and the $\textbf{angular frequency}$ $\omega$ (in rads/s) equals the frequency multiplied by $2\pi$ :