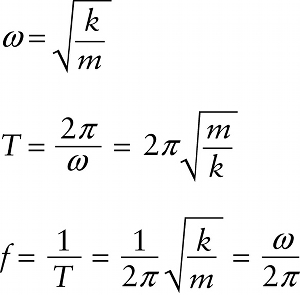Angular frequency, period, and frequency for a block attached to an ideal spring (12-11)

Question 1 of 3

Question

Period

{"title":"Angular frequency","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"2,29,26,53\"}]"} {"title":"Period","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"1,130,25,162\"}]"} {"title":"Frequency","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"poly\",\"coords\":\"132,99\"},{\"shape\":\"rect\",\"coords\":\"1,237,20,275\"}]"}

Review

We’ve seen that the period T of the oscillation in Figure 12-4b is the same as the time $T$ that it takes the object in uniform circular motion in Figure 12-4a to travel once around the circle. The angular speed $\omega$ equals $2\pi/T$ , so $T$ equals $2\pi/\omega$ . Using Equation 12-10 for the value of $\omega$ along with Equation 12-1 for the relationship between period $T$ and frequency $f$ , we get the following results for the oscillations of a block of mass $m$ attached to an ideal, Hooke’s law spring of spring constant $k$ :