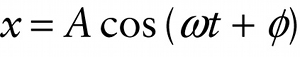Chapter 12. Position as a function of time for simple harmonic motion (12-12)

Review

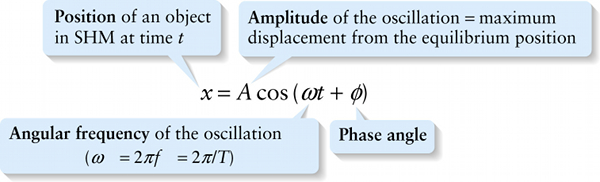
Let’s see what Equation 12-12 tells us. The cosine function has values from \(+1\) to \(-1\). So Equation 12-12 says that the value of \(x\) varies from \(x = A\) (when the oscillating object is at its most positive displacement from equilibrium) through \(x = 0\) (the equilibrium position) to \(x = -A\) (when the object is at its most negative displacement from equilibrium). The cosine is one of the simplest of all oscillating functions, which helps justify the name \(\textit{simple}\) harmonic motion. The cosine and sine functions are called \(\textbf{sinusoidal functions}\) (from the Latin word \(\textit{sinus}\), meaning “bent” or “curved”) because of their shape.

The angular frequency \(\omega\) is measured in rad/s and time \(t\) is measured in \(s\), so the product \(\omega{t}\) in Equation 12-12 is in radians—just as the argument of the cosine function should be. One cycle of oscillation lasts a time \(T\), over which time the product \(\omega{t}\) varies from \(0\) at \(t=0\) to \(\omega{T}\) at \(t=T\). But since\(T = 2\pi/\omega\) from the second of Equations 12-11, it follows that \(\omega{T} = \omega(2\pi/\omega) = 2\pi\). So over the course of one cycle the value of \(\omega{t}\) varies from 0 to \(\omega{T}) = 2\pi\). The cosine function goes through one complete cycle when its value increases by \(2\pi\), so this tells us that the position \(x\) goes through one complete cycle when the time increases by \(T\). That’s just what we mean by saying that \(T\) is the period of the oscillation.

The one quantity in Equation 12-12 that seems a bit mysterious is the \(\textbf{phase angle}\) \(\phi\), which is measured in radians. To explain its significance, recall from our comparison between uniform circular motion and oscillation that \(\phi\) represents the angular position at \(t = 0\) of an object in uniform circular motion. For oscillation, the value of \(\phi\) tells us where in the oscillation cycle the object is at \(t = 0\).