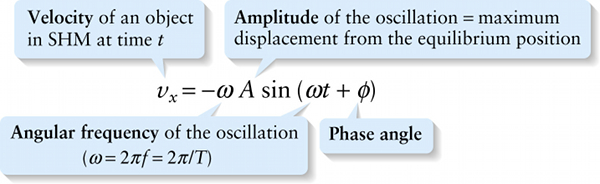
Velocity as a function of time for simple harmonic motion (12-14)

Question 1 of 4

Question

$\textbf{Angular frequency}$ of the oscillation ( $\omega = 2\pi{f} = 2\pi/T$ )

{"title":"Velocity of an object in SHM at time t","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,4,15,23\"}]"} {"title":"Amplitude of the oscillation = maximum displacement from the equilibrium position","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"83,0,105,23\"}]"} {"title":"Phase angle","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"poly\",\"coords\":\"132,99\"},{\"shape\":\"rect\",\"coords\":\"197,1,219,27\"}]"} {"title":"Angular frequency of the oscillation (ω = 2πf = 2π/T)","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"151,2,170,24\"},{\"shape\":\"rect\",\"coords\":\"60,3,83,23\"}]"}

Question

$\textbf{Amplitude}$ of the oscillation = maximum displacement from the equilibrium position

{"title":"Velocity of an object in SHM at time t","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,4,15,23\"}]"} {"title":"Amplitude of the oscillation = maximum displacement from the equilibrium position","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"83,0,105,23\"}]"} {"title":"Phase angle","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"poly\",\"coords\":\"132,99\"},{\"shape\":\"rect\",\"coords\":\"197,1,219,27\"}]"} {"title":"Angular frequency of the oscillation (ω = 2πf = 2π/T)","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"151,2,170,24\"},{\"shape\":\"rect\",\"coords\":\"60,3,83,23\"}]"}

Question

$\textbf{Velocity}$ of an object in SHM at time $t$

{"title":"Velocity of an object in SHM at time t","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,4,15,23\"}]"} {"title":"Amplitude of the oscillation = maximum displacement from the equilibrium position","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"83,0,105,23\"}]"} {"title":"Phase angle","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"poly\",\"coords\":\"132,99\"},{\"shape\":\"rect\",\"coords\":\"197,1,219,27\"}]"} {"title":"Angular frequency of the oscillation (ω = 2πf = 2π/T)","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"151,2,170,24\"},{\"shape\":\"rect\",\"coords\":\"60,3,83,23\"}]"}

Question

$\textbf{Phase angle}$

{"title":"Velocity of an object in SHM at time t","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,4,15,23\"}]"} {"title":"Amplitude of the oscillation = maximum displacement from the equilibrium position","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"83,0,105,23\"}]"} {"title":"Phase angle","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"poly\",\"coords\":\"132,99\"},{\"shape\":\"rect\",\"coords\":\"197,1,219,27\"}]"} {"title":"Angular frequency of the oscillation (ω = 2πf = 2π/T)","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"151,2,170,24\"},{\"shape\":\"rect\",\"coords\":\"60,3,83,23\"}]"}

Review

So for an object in simple harmonic motion the value of the phase angle $\phi$ tells you the point in the oscillation cycle that corresponds to $t = 0$ . Note that Figures 12-6a and 12-6b really depict the same oscillation, with the same amplitude $A$ and period $T$ ; the only difference is the point in the cycle that we call $t = 0$ .

The phase angle also appears in the expressions for velocity and acceleration in simple harmonic motion (Equations 12-7 and 12-8), which we found by analogy with uniform circular motion: