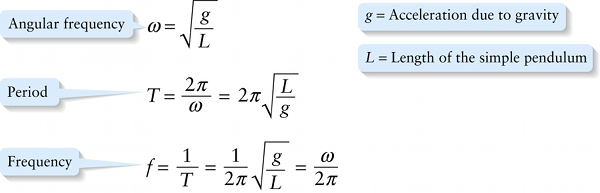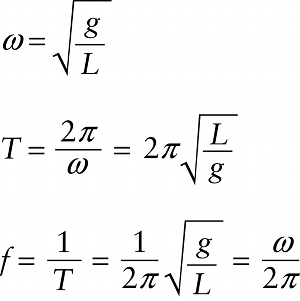Loading [MathJax]/jax/output/HTML-CSS/jax.js

Angular frequency, period, and frequency for a simple pendulum (small amplitude) (12-27)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

Angular frequency
Feedback
{"title":"Angular frequency","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,32,23,53\"}]"} {"title":"Period","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"3,135,21,159\"}]"} {"title":"Frequency","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"1,240,21,276\"}]"}

Review

As in Section 12-3, the period T is equal to 2π / ω and the frequency f is equal to 1 / T or ω / 2π. So we can write the following results for the small-amplitude oscillations of a simple pendulum: