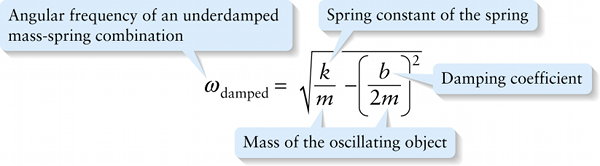
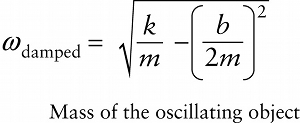Angular frequency of an underdamped oscillation (12-36)
Question 1 of 4
Question
Mass of the oscillating object
{"title":"Angular frequency of an underdamped mass-spring combination","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"3,34,20,56\"}]"} {"title":"Spring constant of the spring","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"141,11,159,41\"}]"} {"title":"Damping coefficient","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"214,12,231,35\"}]"} {"title":"Mass of the oscillating object","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"220,49,245,67\"},{\"shape\":\"rect\",\"coords\":\"137,52,162,69\"}]"}Review
Figure 12-16 is a graph of this function. The decreasing amplitude means that the oscillating object makes smaller and smaller excursions around the equilibrium position as time goes by.
The presence of the damping force also changes the oscillation angular frequency from the value ω=√k/m without damping. With damping present, the angular frequency is